
【题目】已知(x+1)n=a0+a1(x﹣1)+a2(x﹣1)2+a3(x﹣1)3+…+an(x﹣1)n , (其中n∈N*)
(1)求a0及Sn=a1+2a2+3a3+…+nan;
(2)试比较Sn与n3的大小,并说明理由.
【答案】
(1)解:取x=1,可得 ![]() .
.
对等式两边求导,得 ![]() ,
,
取x=2,则 ![]()
(2)解:要比较Sn与n3的大小,即比较:3n﹣1与n2的大小,
当n=1,2时,3n﹣1<n2; 当n=3时,3n﹣1=n2;当n=4,5时,3n﹣1>n2.
猜想:当n≥4时,3n﹣1>n2,下面用数学归纳法证明:
由上述过程可知,n=4时结论成立,
假设当n=k,(k≥4)时结论成立,即3k﹣1>k2,
当n=k+1时,3(k+1)﹣1=33k﹣1>3k2.
而3k2﹣(k+1)2=2k2﹣2k﹣1=2k(k﹣1)﹣1≥2×4×3﹣1=23>0,
∴3(k+1)﹣1>33k﹣1>3k2>(k+1)2,故当n=k+1时结论也成立,
∴当n≥4时,3n﹣1>n2成立.
综上得,当n=1,2时, ![]() ; 当n=3时,
; 当n=3时, ![]() ;当n≥4,n∈N*时,
;当n≥4,n∈N*时, ![]()
【解析】(1)取x=1,即可求得 a0的值.对所给的等式两边求导,再取x=2,可得Sn的值.(2)要比较Sn与n3的大小,即比较:3n﹣1与n2的大小,当n=1,2时,3n﹣1<n2; 当n=3时,3n﹣1=n2; 当n=4,5时,3n﹣1>n2 . 猜想:当n≥4时,3n﹣1>n2 , 再用数学归纳法证明.
【考点精析】通过灵活运用数列的前n项和,掌握数列{an}的前n项和sn与通项an的关系 即可以解答此题.
即可以解答此题.


科目:高中数学 来源: 题型:
【题目】在统计学中,偏差是指个别测定值与测定的平均值之差,在成绩统计中,我们把某个同学的某刻考试成绩与该科班平均分的差叫某科偏差,班主任为了了解个别学生的偏科情况,对学生数学偏差![]() (单位:分)与物理偏差
(单位:分)与物理偏差![]() (单位:分)之间的关系进行偏差分析,决定从全班40位同学中随机抽取一个容量为8的样本进行分析,得到他们的两科成绩偏差数据如表:
(单位:分)之间的关系进行偏差分析,决定从全班40位同学中随机抽取一个容量为8的样本进行分析,得到他们的两科成绩偏差数据如表:

(1)已知![]() 与
与![]() 之间具有线性相关关系,求
之间具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)若这次考试该班数学平均分为120分,物理平均分为92,试预测数学成绩126分的同学的物理成绩.
参考公式:  ,
, ![]()
参考数据: ![]() ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的函数 ![]() .
.
(1)如果函数 ![]() ,求b、c;
,求b、c;
(2)设当x∈( ![]() ,3)时,函数y=f(x)﹣c(x+b)的图象上任一点P处的切线斜率为k,若k≤2,求实数b的取值范围.
,3)时,函数y=f(x)﹣c(x+b)的图象上任一点P处的切线斜率为k,若k≤2,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)求函数![]() 的单调递增区间;
的单调递增区间;
(Ⅱ)把![]() 的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移
的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象,求
的图象,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的顶点A(5,1),AB边上的中线CM所在直线方程为2x﹣y﹣5=0,∠B的平分线BN所在直线方程为x﹣2y﹣5=0.求:
(1)顶点B的坐标;
(2)直线BC的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD﹣A1B1C1D1中,M,N分别是BC1 , CD1的中点,则下列说法错误的是( ) 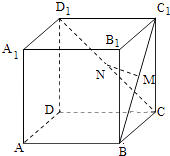
A.MN与CC1垂直
B.MN与AC垂直
C.MN与BD平行
D.MN与A1B1平行
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在点
在点![]() 处的切线为
处的切线为![]() .
.
(1)求实数![]() ,
, ![]() 的值;
的值;
(2)是否存在实数![]() ,当
,当![]() 时,函数
时,函数![]() 的最小值为
的最小值为![]() ,若存在,求出
,若存在,求出![]() 的取值范围;若不存在,说明理由;
的取值范围;若不存在,说明理由;
(3)若![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com