
【题目】已知函数f(x)=ln x-a(x-1),g(x)=ex.
(1)求函数f(x)的单调区间;
(2)若函数h(x)=f(x+1)+g(x),当x>0时,h(x)>1恒成立,求实数a的取值范围.
【答案】(1)见解析(2)(-∞,2]
【解析】分析:(1)由函数![]() ,求得
,求得![]() ,分类讨论即可求解函数的单调区间;
,分类讨论即可求解函数的单调区间;
(2)因为![]() ,所以
,所以![]() ,令
,令![]() ,求得
,求得![]() ,得到
,得到![]() 单调性和最值,即可求解.
单调性和最值,即可求解.
详解:(1)函数f(x)的定义域为(0,+∞),f′(x)=![]() -a=
-a=![]() (x>0)..
(x>0)..
①若a≤0,对任意的x>0,均有f′(x)>0,所以f(x)的单调递增区间为(0,+∞),无单调递减区间;.
②若a>0,当x∈![]() 时,f′(x)>0,当x∈
时,f′(x)>0,当x∈![]() 时,f′(x)<0,所以f(x)的单调递增区间为
时,f′(x)<0,所以f(x)的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ...
...
综上,当a≤0时,f(x)的单调递增区间为(0,+∞),无单调递减区
当a>0时,f(x)的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]()
(2)因为h(x)=f(x+1)+g(x)=ln (x+1)-ax+ex,所以
h′(x)=ex+![]() -a..
-a..
令φ(x)=h′(x),因为x∈(0,+∞),φ′(x)=ex-![]() =
=![]() >0.
>0.
所以h′(x)在(0,+∞)上单调递增,h′(x)>h′(0)=2-a,
①当a≤2时,h′(x)>0,所以h(x)在(0,+∞)上单调递增,h(x)>h(0)=1恒成立,符合题意;.
②当a>2时,h′(0)=2-a<0,h′(x)>h′(0),所以存在x0∈(0,+∞),使得h′(x0)=0..
所以h(x)在(x0,+∞)上单调递增,在(0,x0)上单调递减,又h(x0)<h(0)=1,所以h(x)>1不恒成立,不符合题意.
综上,实数a的取值范围是(-∞,2].


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:高中数学 来源: 题型:
【题目】已知圆![]() ,直线过点
,直线过点![]() ,且
,且![]() ,线段
,线段![]() 交圆
交圆![]() 的交点为点
的交点为点![]() ,
,![]() 是
是![]() 关于轴的对称点.
关于轴的对称点.
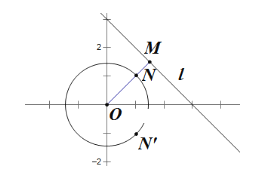
(1)求直线![]() 的方程;
的方程;
(2)已知![]() 是圆
是圆![]() 上不同的两点,且
上不同的两点,且![]() ,试证明直线
,试证明直线![]() 的斜率为定值,并求出该定值.
的斜率为定值,并求出该定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,中美贸易摩擦不断.特别是美国对我国华为的限制.尽管美国对华为极力封锁,百般刁难,并不断加大对各国的施压,拉拢他们抵制华为5G,然而这并没有让华为却步.华为在2018年不仅净利润创下记录,海外增长同样强劲.今年,我国华为某一企业为了进一步增加市场竞争力,计划在2020年利用新技术生产某款新手机.通过市场分析,生产此款手机全年需投入固定成本250万,每生产![]() (千部)手机,需另投入成本
(千部)手机,需另投入成本![]() 万元,且
万元,且  ,由市场调研知,每部手机售价0.7万元,且全年内生产的手机当年能全部销售完.
,由市场调研知,每部手机售价0.7万元,且全年内生产的手机当年能全部销售完.
(![]() )求出2020年的利润
)求出2020年的利润![]() (万元)关于年产量
(万元)关于年产量![]() (千部)的函数关系式,(利润=销售额—成本);
(千部)的函数关系式,(利润=销售额—成本);
![]() 2020年产量为多少(千部)时,企业所获利润最大?最大利润是多少?
2020年产量为多少(千部)时,企业所获利润最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
最高气温 | [10,15) | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) |
天数 | 2 | 16 | 36 | 25 | 7 | 4 |
以最高气温位于各区间的频率代替最高气温位于该区间的概率.
(Ⅰ)求六月份这种酸奶一天的需求量X(单位:瓶)的分布列;
(Ⅱ)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量n(单位:瓶)为多少时,Y的数学期望达到最大值?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】研究发现,北京 PM 2.5 的重要来源有土壤尘、燃煤、生物质燃烧、汽车尾气与垃圾焚烧、工业污染和二次无机气溶胶,其中燃煤的平均贡献占比约为 18%.为实现“节能减排”,还人民“碧水蓝天”,北京市推行“煤改电”工程,采用空气源热泵作为冬天供暖.进入冬季以来,该市居民用电量逐渐增加,为保证居民取暖,市供电部门对该市 100 户居民冬季(按 120 天计算)取暖用电量(单位:度)进行统计分析,得到居民冬季取暖用电量的频率分布直方图如图所示.

(1)求频率分布直方图中![]() 的值;
的值;
(2)从这 100 户居民中随机抽取 1 户进行深度调查,求这户居民冬季取暖用电量在[3300,3400]的概率;
(3)在用电量为[3200,3250),[3250,3300),[3300,3350),[3350,3400]的四组居民中,用分层抽样的方法抽取 34 户居民进行调查,则应从用电量在[3200,3250)的居民中抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)(x∈R)满足f(x)=f(2-x),且对任意的x1,x2∈(-∞,1](x1≠x2)有(x1-x2)(f(x1)-f(x2))<0.则( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,其中AD∥BC,AB⊥AD,AB=AD= ![]() BC,
BC, ![]() =
= ![]()
![]() .
. 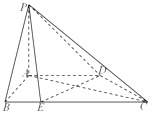
(1)求证:DE⊥平面PAC;
(2)若直线PE与平面PAC所成角的正弦值为 ![]() ,求二面角A﹣PC﹣D的平面角的余弦值.
,求二面角A﹣PC﹣D的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}共有5项,其中a1=0,a5=2,且|ai+1﹣ai|=1,i=1,2,3,4,则满足条件的不同数列的个数为( )
A.3
B.4
C.5
D.6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com