
 ,现有3名学生从中任选一个科目参加学习(互不影响),记
,现有3名学生从中任选一个科目参加学习(互不影响),记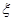 为3人中选择的科目属于“文学”或“竞赛”的人数,求
为3人中选择的科目属于“文学”或“竞赛”的人数,求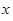 的分布列及期望。
的分布列及期望。科目:高中数学 来源:不详 题型:解答题
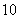 个编号为
个编号为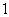 、
、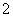 、
、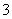 的球,
的球,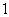 号球有
号球有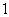 个,
个,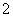 号球有
号球有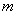 个,
个,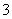 号球有
号球有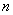 个.从袋中依次摸出
个.从袋中依次摸出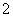 个球,已知在第一次摸出
个球,已知在第一次摸出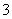 号球的前提下,再摸出一个
号球的前提下,再摸出一个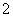 号球的概率是
号球的概率是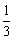 .
.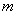 、
、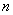 的值;
的值;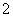 个球,记得到小球的编号数之和为
个球,记得到小球的编号数之和为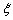 ,求随机变量
,求随机变量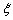 的分布列和数学期望
的分布列和数学期望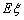 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 分组 | 频数 | 频率 |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
| 合计 |  |  |
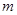 、
、 、
、 、
、 的值,并根据表中所给数据在下面给出的坐标系中画出频率分布直方图;
的值,并根据表中所给数据在下面给出的坐标系中画出频率分布直方图;
 分以上的人数;
分以上的人数;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
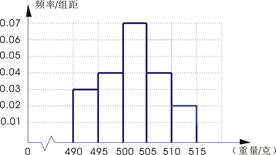
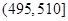 的产品为合格品,否则为不合格品.表1是甲流水线样本频数分布表,图1是乙流水线样本的频率分布直方图.
的产品为合格品,否则为不合格品.表1是甲流水线样本频数分布表,图1是乙流水线样本的频率分布直方图.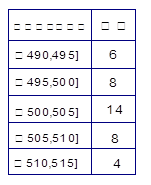
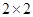 列联表,并回答有多大的把握认为“产品的包装质量与两条自动包装流水线的选择有关”.
列联表,并回答有多大的把握认为“产品的包装质量与两条自动包装流水线的选择有关”.| | 甲流水线 | 乙流水线 | 合计 |
| 合格品 | 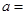 | 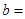 | |
| 不合格品 | 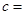 | 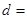 | |
| 合 计 | | | 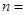 |
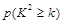 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
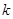 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
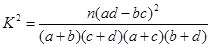 ,其中
,其中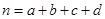 )
)
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 登记所需时间(分) | 1 | 2 | 3 | 4 | 5 |
| 频率 | 0.1 | 0.4 | 0.3 | 0.1 | 0.1 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
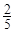 小时,种植一棵枫树苗用时
小时,种植一棵枫树苗用时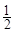 小时.完成这次植树任务需要最短时间为( )
小时.完成这次植树任务需要最短时间为( )A.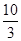 | B.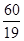 | C.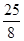 | D.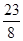 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
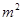 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com