
【题目】已知函数![]() .
.
(1)若![]() 在其定义域上单调递减,求
在其定义域上单调递减,求![]() 的取值范围;
的取值范围;
(2)证明:![]() 在区间
在区间![]() 恰有一个零点.
恰有一个零点.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1) ![]() ,如果
,如果![]() 单调递减,则当
单调递减,则当![]() 时,
时,![]() 恒成立,可求出答案.
恒成立,可求出答案.
(2) 当![]() 时,由于
时,由于![]() 在区间
在区间![]() 单调递减,且
单调递减,且![]() ,
,![]() ,命题成立. 当
,命题成立. 当![]() 时,由于
时,由于![]() ,方程
,方程![]() 在区间
在区间![]() 有唯一的实根
有唯一的实根![]() ,从而
,从而![]() 在区间
在区间![]() 单调递减,在区间
单调递减,在区间![]() 单调递增,可以讨论得到命题的证明.
单调递增,可以讨论得到命题的证明.
(1)由于![]() 的定义域为
的定义域为![]() ,且
,且![]() ,所以如果
,所以如果![]() 单调递减,则当
单调递减,则当![]() 时,
时,![]() 恒成立,解得
恒成立,解得![]() ,即
,即![]() 的取值范围为
的取值范围为![]() .
.
(2)(i)当![]() 时,由于
时,由于![]() 在区间
在区间![]() 单调递减,且
单调递减,且![]() ,
,
![]() ,所以
,所以![]() 区间
区间![]() 恰有一个零点;
恰有一个零点;
(ii)当![]() 时,由于
时,由于![]() ,
,
由![]() ,设
,设![]() ,
,
对称轴为![]() ,
,![]() ,且
,且![]() .
.
所以方程![]() 在区间
在区间![]() 有唯一的实根
有唯一的实根![]() ,
,
从而![]() 在区间
在区间![]() 单调递减,在区间
单调递减,在区间![]() 单调递增,注意到
单调递增,注意到![]() ,
,
所以![]() 区间
区间![]() 的零点个数不超过1个.
的零点个数不超过1个.
①当![]() 时,由于
时,由于![]() ,所以
,所以![]() 区间
区间![]() 恰有一个零点;
恰有一个零点;
②当![]() 时,由于
时,由于![]() ,所以
,所以![]() 区间
区间![]() 恰有一个零点.
恰有一个零点.
综上,![]() 在区间
在区间![]() 恰有一个零点.
恰有一个零点.


科目:高中数学 来源: 题型:
【题目】南充高中扎实推进阳光体育运动,积极引导学生走向操场,走进大自然,参加体育锻炼,每天上午第三节课后全校大课间活动时长35分钟.现为了了解学生的体育锻炼时间,采用简单随机抽样法抽取了100名学生,对其平均每日参加体育锻炼的时间(单位:分钟)进行调查,按平均每日体育锻炼时间分组统计如下表:
分组 |
|
|
|
|
|
|
男生人数 | 2 | 16 | 19 | 18 | 5 | 3 |
女生人数 | 3 | 20 | 10 | 2 | 1 | 1 |
若将平均每日参加体育锻炼的时间不低于120分钟的学生称为“锻炼达人”.
(1)将频率视为概率,估计我校7000名学生中“锻炼达人”有多少?
(2)从这100名学生的“锻炼达人”中按性别分层抽取5人参加某项体育活动.
①求男生和女生各抽取了多少人;
②若从这5人中随机抽取2人作为组长候选人,求抽取的2人中男生和女生各1人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个结论:
①若![]() 在
在![]() 上是奇函数,则
上是奇函数,则![]() 在
在![]() 上也是奇函数
上也是奇函数
②若![]() 不是正弦函数,则
不是正弦函数,则![]() 不是周期函数
不是周期函数
③“若![]() ,则
,则![]() .”的否命题是“若
.”的否命题是“若![]() ,则
,则![]() .”
.”
④若![]() :
:![]() ;
;![]() :
:![]() ,则
,则![]() 是
是![]() 的充分不必要条件
的充分不必要条件
其中正确结论的个数为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
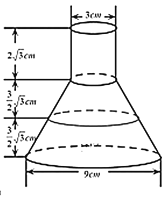
【题目】《乌鸦喝水》是《伊索寓言》中一个寓言故事,通过讲述已知乌鸦喝水的故事,告诉人们遇到困难要运用智慧,认真思考才能让问题迎刃而解的道理,如图![]() 所示,乌鸦想喝水,发现有一个锥形瓶,上面部分是圆柱体,下面部分是圆台,瓶口直径为
所示,乌鸦想喝水,发现有一个锥形瓶,上面部分是圆柱体,下面部分是圆台,瓶口直径为![]() 厘米,瓶底直径为
厘米,瓶底直径为![]() 厘米,瓶口距瓶颈为
厘米,瓶口距瓶颈为![]() 厘米,瓶颈到水位线距离和水位线到瓶底距离均为
厘米,瓶颈到水位线距离和水位线到瓶底距离均为![]() 厘米,现将
厘米,现将![]() 颗石子投入瓶中,发现水位线上移
颗石子投入瓶中,发现水位线上移![]() 厘米,若只有当水位线到达瓶口时乌鸦才能喝到水,则乌鸦共需要投入的石子数量至少是( )
厘米,若只有当水位线到达瓶口时乌鸦才能喝到水,则乌鸦共需要投入的石子数量至少是( )
A.![]() 颗B.
颗B.![]() 颗C.
颗C.![]() 颗D.
颗D.![]() 颗
颗
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)设各项均为正数的等比数列![]() 中,
中,![]()
![]()
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,求证:
,求证: ![]() ;
;
(3)是否存在正整数![]() ,使得
,使得![]() 对任意正整数
对任意正整数![]() 均成立?若存在,求出
均成立?若存在,求出![]() 的最大值,若不存在,说明理由.
的最大值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,C是半圆O上除A,B外的一个动点,DC垂直于半圆O所在的平面,DC∥EB,DC=EB=1,AB=4.
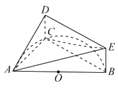
(1)证明:平面ADE⊥平面ACD;
(2)当C点为半圆的中点时,求二面角D﹣AE﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面上到两个定点的距离的积为定值的动点轨迹一般称为卡西尼(cassin)卵形线,已知曲线![]() 为到定点
为到定点![]() 的距离之积为常数4的点
的距离之积为常数4的点![]() 的轨迹,关于曲线
的轨迹,关于曲线![]() 的几何性质有下四个结论,其中错误的是( )
的几何性质有下四个结论,其中错误的是( )
A.曲线![]() 关于原点对称B.
关于原点对称B.![]() 的面积的最大值为2
的面积的最大值为2
C.其中![]() 的取值范围为
的取值范围为![]() D.其中
D.其中![]() 的取值范围为
的取值范围为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年春,新型冠状病毒在我国湖北武汉爆发并讯速蔓延,病毒传染性强并严重危害人民生命安全,国家卫健委果断要求全体人民自我居家隔离,为支援湖北武汉新型冠状病毒疫情防控工作,各地医护人员纷纷逆行,才使得病毒蔓延得到了有效控制.某社区为保障居民的生活不受影响,由社区志愿者为其配送蔬菜、大米等生活用品,记者随机抽查了男、女居民各100名对志愿者所买生活用品满意度的评价,得到下面的2×2列联表.
特别满意 | 基本满意 | |
男 | 80 | 20 |
女 | 95 | 5 |
(1)被调查的男性居民中有5个年轻人,其中有2名对志愿者所买生活用品特别满意,现在这5名年轻人中随机抽取3人,求至多有1人特别满意的概率.
(2)能否有99%的把握认为男、女居民对志愿者所买生活用品的评价有差异?
附: 
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com