【题目】已知某校甲、乙、丙三个兴趣小组的学生人数分别为36，24，12.现采用分层抽样的方法从中抽取6人，进行睡眠质量的调查.
（1）应从甲、乙、丙三个兴趣小组的学生中分别抽取多少人？
（2）设抽出的6人分别用
、
、
、
、
、
表示，现从6人中随机抽取2人做进一步的身体检查.
（i）试用所给字母列出所有可能的抽取结果；
（ii）设
为事件“抽取的2人来自同一兴趣小组”，求事件发生的概率.
【答案】（1）3人、2人、1人.（2）（i）见解析（ii）
【解析】
（1）先算出甲、乙、丙三个兴趣小组的学生人数之比，再采用分层抽样的方法抽取.
（2）（i）从抽出的6人中随机抽取2人的所有可能结果用列举法列出.（ii）对6人进行编号，来自甲兴趣小组的是
，
，
，来自乙兴趣小组的是
，
，来自丙兴趣小组的是
，再列举则从6人中随机抽取2人来自同一兴趣小组的可能结果，用古典概型的概率.
（1）由已知，甲、乙、丙三个兴趣小组的学生人数之比为
，
由于采用分层抽样的方法从中抽取6人，因此从甲、乙、丙三个兴趣小组中分别抽取3人、2人、1人.
（2）（i）从抽出的6人中随机抽取2人的所有可能结果为：
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，共15种.
（ii）不妨设抽出的6人中，来自甲兴趣小组的是，，，来自乙兴趣小组的是，，来自丙兴趣小组的是，则从6人中随机抽取2人来自同一兴趣小组的可能结果为，，，，共4种.
所以，事件
发生的概率
.
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案科目：高中数学 来源： 题型：
【题目】如图，
是抛物线
的焦点，过点且与坐标轴不垂直的直线交抛物线于
、
两点，交抛物线的准线于点
，其中
，
．过点作
轴的垂线交抛物线于点
，直线
交抛物线于点
.
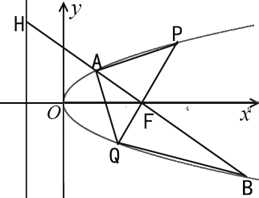
（1）求
的值；
（2）求四边形
的面积
的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，已知三棱柱
中，
底面
，
，
，
，
.
，
分别为棱
，
的中点.
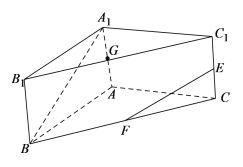
（1）求异面直线
与
所成角的大小；
（2）若
为线段
的中点，试在图中作出过、、三点的平面截该棱柱所得的多边形，并求出以该多边形为底，
为顶点的棱锥的体积.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图1，在直角梯形ABCD中，
，
，
，四边形ABEF是正方形.将正方形ABEF沿AB折起到四边形
的位置，使平面
平面ABCD，M为
的中点，如图2.
图1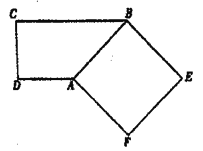
图2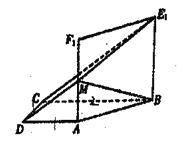
（1）求证:
；
（2）求平面
与平面所成锐二面角的余弦值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】定义：若无穷数列
满足
是公比为
的等比数列，则称数列为“
数列”.设数列
中
（1）若
，且数列是“数列”，求数列的通项公式；
（2）设数列的前
项和为
，且
，请判断数列是否为“数列”，并说明理由；
（3）若数列是“
数列”，是否存在正整数
，使得
？若存在，请求出所有满足条件的正整数；若不存在，请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
