
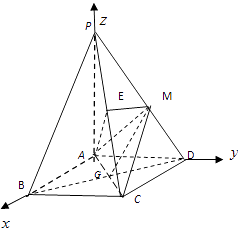
【题目】如图,四棱锥P﹣ABCD的底面是正方形,PA⊥底面ABCD,PA=AD,点M是PD的中点,作ME⊥PC,交PC于点E. 
(1)求证:PB∥平面MAC;
(2)求证:PC⊥平面AEM;
(3)求二面角A﹣PC﹣D的大小.
【答案】
(1)证明:如图建立空间直角坐标系D﹣xyz,设AD=1.
![]() ,
, ![]() ,所以
,所以 ![]() ,
,
即PB∥MG,因此,PB∥平面MAC
(2)证明: ![]() ,
, ![]() ,
,
故 ![]() ,
,
所以PC⊥AM,又PC⊥EM,
所以 PC⊥平面AEM
(3)解:由(2)知PC⊥AE,故MEA是二面角A﹣PC﹣D的平面角.
设E=(x,y,z),则 ![]() .因为
.因为 ![]() ,
,
所以(x,y,z﹣1)=k(1,1,﹣1),
即x=k,y=k,z=1﹣k.
所以 ![]() ,
,
所以k= ![]() ,点
,点 ![]() .
.
又点 ![]() ,所以
,所以 ![]() ,
, ![]() =(
=( ![]() ,
, ![]() ,﹣
,﹣ ![]() ),
),
故  ,
,
所以∠MEA=60°,即二面角A﹣PC﹣D的大小为60°
【解析】(1)建立空间坐标系,求出直线对应的向量,利用向量法即可证明PB∥平面MAC;(2)根据线面垂直的判定定理结合向量法即可证明PC⊥平面AEM;(3)根据二面角的定义作出二面角的平面角,结合向量即可求二面角A﹣PC﹣D的大小.
【考点精析】关于本题考查的直线与平面平行的判定和直线与平面垂直的判定,需要了解平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】已知全集为全体实数R,集合A={x|3≤x≤7},B={x|2<x<10},C={x|x<a}.
(1)求(RA)∩B;
(2)若A∩C≠,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD= ![]() ,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点. 
(1)求证:PO⊥平面ABCD;
(2)求异面直线PB与CD所成角的余弦值;
(3)线段AD上是否存在点Q,使得它到平面PCD的距离为 ![]() ?若存在,求出
?若存在,求出 ![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下茎叶图记录了甲、乙两个篮球队在3次不同比赛中的得分情况.乙队记录中有一个数字模糊,无法确认,假设这个数字具有随机性,并在图中以m表示.那么在3次比赛中,乙队平均得分超过甲队平均得分的概率是( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:存在x∈(﹣∞,1)使得x2﹣4x+m=0成立,命题q:方程 ![]() 表示焦点在x轴上的椭圆.
表示焦点在x轴上的椭圆.
(1)若p是真命题,求实数m的取值范围;
(2)若p或q是假命题,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数 ![]() ,曲线y=f(x)在点(2,f(2))处的切线方程为7x﹣4y﹣12=0.
,曲线y=f(x)在点(2,f(2))处的切线方程为7x﹣4y﹣12=0.
(1)求y=f(x)的解析式;
(2)证明:曲线y=f(x)上任一点处的切线与直线x=0和直线y=x所围成的三角形面积为定值,并求此定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com