
【答案】(1)![]() ;(2)单调递增区间为
;(2)单调递增区间为![]() ;单调递减区间为
;单调递减区间为![]() ;(3)详见解析.
;(3)详见解析.
【解析】
试题分析:(1)根据题意分析可能曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴平行,等价于
轴平行,等价于![]() ,从而
,从而![]() ;(2)由(1)可知
;(2)由(1)可知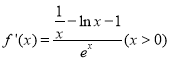 ,只需考虑分子
,只需考虑分子![]() 的正负性即可,而
的正负性即可,而![]() ,
,![]() 在
在![]() 上单调递减,再由
上单调递减,再由![]() ,故当
,故当![]() 时,
时,![]() ,
,![]() ,
,![]() 单调递增;当
单调递增;当![]() 时,
时,![]() ,
,![]() ,
,![]() 单调递减,∴单调递增区间为
单调递减,∴单调递增区间为![]() ;单调递减区间为
;单调递减区间为![]() ;(3)
;(3)![]() ,这是一指对相结合的函数,混在一起考虑其单调性比较复杂,因此考虑分开研究各自的取值情况:记
,这是一指对相结合的函数,混在一起考虑其单调性比较复杂,因此考虑分开研究各自的取值情况:记![]() ,
,![]() ,
,![]() ,令
,令![]() ,得
,得![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递增;当
单调递增;当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
∴![]() ,即
,即![]() .
.
② 记![]() ,
,![]() ,
,![]() ,∴
,∴![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() ,即
,即![]() ,综合①,②可知,
,综合①,②可知,![]() .
.
试题解析:(1)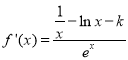 ,依题意,
,依题意,![]() 为所求;
为所求;
(2)由(1)可知,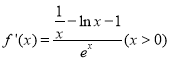 ,记
,记![]() ,
,![]() ,
,
∴![]() 在
在![]() 上单调递减,又∵
上单调递减,又∵![]() ,
,
∴当![]() 时,
时,![]() ,
,![]() ,
,![]() 单调递增;当
单调递增;当![]() 时,
时,![]() ,
,![]() ,
,![]() 单调递减,∴单调递增区间为
单调递减,∴单调递增区间为![]() ;单调递减区间为
;单调递减区间为![]() ;
;
(3)![]() ,
,
① 记![]() ,
,![]() ,
,![]() ,令
,令![]() ,得
,得![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递增;当
单调递增;当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
∴![]() ,即
,即![]() .
.
② 记![]() ,
,![]() ,
,![]() ,∴
,∴![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() ,即
,即![]() ,综合①,②可知,
,综合①,②可知,![]() .
.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ax2﹣(2a+1)x+2lnx(a∈R).
ax2﹣(2a+1)x+2lnx(a∈R).
(1)当a=1时,求函数f(x)的单调区间;
(2)当a>0时,设g(x)=(x2﹣2x)ex , 求证:对任意x1∈(0,2],均存在x2∈(0,2],使得f(x1)<g(x2)成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点, ![]() 轴的正半轴为极轴,建立极坐标系,两坐标系中取相同的单位长度,已知曲线
轴的正半轴为极轴,建立极坐标系,两坐标系中取相同的单位长度,已知曲线![]() 的方程为
的方程为![]() ,点
,点![]() .
.
(1)求曲线![]() 的直角坐标方程和点
的直角坐标方程和点![]() 的直角坐标;
的直角坐标;
(2)设![]() 为曲线
为曲线![]() 上一动点,以
上一动点,以![]() 为对角线的矩形
为对角线的矩形![]() 的一边平行于极轴,求矩形
的一边平行于极轴,求矩形![]() 周长的最小值及此时点
周长的最小值及此时点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的部分图象如图所示.
的部分图象如图所示.
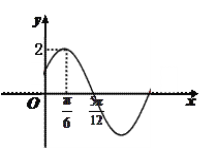
(1) 求函数![]() 的解析式;
的解析式;
(2) 如何由函数![]() 的通过适当图象的变换得到函数
的通过适当图象的变换得到函数![]() 的图象, 写出变换过程;
的图象, 写出变换过程;
(3) 若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知全集U=R,A={x|x≥3},B={x|x2﹣8x+7≤0},C={x|x≥a﹣1}
(1)求A∩B,A∪B;
(2)若A∩C=C,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+alnx. (Ⅰ)当a=﹣2时,求函数f(x)的单调区间和极值;
(Ⅱ)若g(x)=f(x)+ ![]() 在[1,+∞)上是单调增函数,求实数a的取值范围.
在[1,+∞)上是单调增函数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
某工厂有100名工人接受了生产1000台某产品的总任务,每台产品由9个甲型装置和3个乙型装置配套组成,每个工人每小时能加工完成1个甲型装置或3个乙型装置.现将工人分成两组分别加工甲型和乙型装置.设加工甲型装置的工人有x人,他们加工完甲型装置所需时间为t1小时,其余工人加工完乙型装置所需时间为t2小时.
设f(x)=t1+t2.
(Ⅰ)求f(x)的解析式,并写出其定义域;
(Ⅱ)当x等于多少时,f(x)取得最小值?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中秋节即将到来,为了做好中秋节商场促销活动,某商场打算将进行促销活动的礼品盒重新设计.方案如下:将一块边长为10的正方形纸片![]() 剪去四个全等的等腰三角形
剪去四个全等的等腰三角形![]() ,
, ![]() ,
, ![]() ,
, ![]() 再将剩下的阴影部分折成一个四棱锥形状的包装盒
再将剩下的阴影部分折成一个四棱锥形状的包装盒![]() ,其中
,其中![]() 重合于点
重合于点![]() ,
, ![]() 与
与![]() 重合,
重合, ![]() 与
与![]() 重合,
重合, ![]() 与
与![]() 重合,
重合, ![]() 与
与![]() 重合(如图所示).
重合(如图所示).
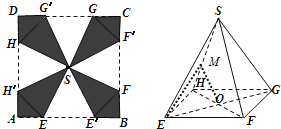
(1)求证:平面![]() 平面
平面![]() ;
;
(2)已知![]() ,过
,过![]() 作
作![]() 交
交![]() 于点
于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com