
【题目】已知抛物线Γ:y2=2px(p>0)的焦点为F,P是抛物线Γ上一点,且在第一象限,满足![]() (2,2
(2,2![]() )
)
(1)求抛物线Γ的方程;
(2)已知经过点A(3,﹣2)的直线交抛物线Γ于M,N两点,经过定点B(3,﹣6)和M的直线与抛物线Γ交于另一点L,问直线NL是否恒过定点,如果过定点,求出该定点,否则说明理由.
【答案】(1)y2=4x;;(2)直线NL恒过定点(﹣3,0),理由见解析.
【解析】
(1)根据抛物线的方程,求得焦点F(![]() ,0),利用
,0),利用![]() (2,2
(2,2![]() ),表示点P的坐标,再代入抛物线方程求解.
),表示点P的坐标,再代入抛物线方程求解.
(2)设M(x0,y0),N(x1,y1),L(x2,y2),表示出MN的方程y![]() 和ML的方程y
和ML的方程y![]() ,因为A(3,﹣2),B(3,﹣6)在这两条直线上,分别代入两直线的方程可得y1y2=12,然后表示直线NL的方程为:y﹣y1
,因为A(3,﹣2),B(3,﹣6)在这两条直线上,分别代入两直线的方程可得y1y2=12,然后表示直线NL的方程为:y﹣y1![]() (x
(x![]() ),代入化简求解.
),代入化简求解.
(1)由抛物线的方程可得焦点F(![]() ,0),满足
,0),满足![]() (2,2
(2,2![]() )的P的坐标为(2
)的P的坐标为(2![]() ,2
,2![]() ),P在抛物线上,
),P在抛物线上,
所以(2![]() )2=2p(2
)2=2p(2![]() ),即p2+4p﹣12=0,p>0,解得p=2,所以抛物线的方程为:y2=4x;
),即p2+4p﹣12=0,p>0,解得p=2,所以抛物线的方程为:y2=4x;
(2)设M(x0,y0),N(x1,y1),L(x2,y2),则y12=4x1,y22=4x2,
直线MN的斜率kMN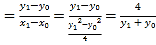 ,
,
则直线MN的方程为:y﹣y0![]() (x
(x![]() ),
),
即y![]() ①,
①,
同理可得直线ML的方程整理可得y![]() ②,
②,
将A(3,﹣2),B(3,﹣6)分别代入①,②的方程
可得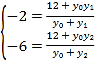 ,消y0可得y1y2=12,
,消y0可得y1y2=12,
易知直线kNL![]() ,则直线NL的方程为:y﹣y1
,则直线NL的方程为:y﹣y1![]() (x
(x![]() ),
),
即y![]() x
x![]() ,故y
,故y![]() x
x![]() ,
,
所以y![]() (x+3),
(x+3),
因此直线NL恒过定点(﹣3,0).


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 的顶点在原点,且该抛物线经过点
的顶点在原点,且该抛物线经过点![]() ,其焦点
,其焦点![]() 在
在![]() 轴上.
轴上.
(Ⅰ)求过点![]() 且与直线
且与直线![]() 垂直的直线的方程;
垂直的直线的方程;
(Ⅱ)设过点![]() 的直线交抛物线
的直线交抛物线![]() 于
于![]() ,
,![]() 两点,
两点,![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴为
的长轴为![]() ,且点
,且点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知点![]() ,若点
,若点![]() 为椭圆
为椭圆![]() 上一动点(不同于点
上一动点(不同于点![]() 、
、![]() )直线
)直线![]() .设直线
.设直线![]() 的方程为
的方程为![]() ,直线
,直线![]() 与直线
与直线![]() 、
、![]() 、
、![]() 分别交于
分别交于![]() 、
、![]() 、
、![]() 三点,试问:是否存在实数
三点,试问:是否存在实数![]() ,使得
,使得![]() 恒成立?若存在,请求出实数
恒成立?若存在,请求出实数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电视台举行一个比赛类型的娱乐节目, ![]() 两队各有六名选手参赛,将他们首轮的比赛成绩作为样本数据,绘制成茎叶图如图所示,为了增加节目的趣味性,主持人故意将
两队各有六名选手参赛,将他们首轮的比赛成绩作为样本数据,绘制成茎叶图如图所示,为了增加节目的趣味性,主持人故意将![]() 队第六位选手的成绩没有给出,并且告知大家
队第六位选手的成绩没有给出,并且告知大家![]() 队的平均分比
队的平均分比![]() 队的平均分多4分,同时规定如果某位选手的成绩不少于21分,则获得“晋级”.
队的平均分多4分,同时规定如果某位选手的成绩不少于21分,则获得“晋级”.
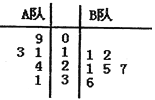
(1)根据茎叶图中的数据,求出![]() 队第六位选手的成绩;
队第六位选手的成绩;
(2)主持人从![]() 队所有选手成绩中随机抽2个,求至少有一个为“晋级”的概率;
队所有选手成绩中随机抽2个,求至少有一个为“晋级”的概率;
(3)主持人从![]() 两队所有选手成绩分别随机抽取2个,记抽取到“晋级”选手的总人数为
两队所有选手成绩分别随机抽取2个,记抽取到“晋级”选手的总人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司准备加大对一项产品的科技改造,经过充分的市场调研与模拟,得到x,y之间的一组数,其中x(单位:百万元)是科技改造的总投入,y(单位:百万元)是改造后的额外收益
x | 2 | 3 | 5 | 7 | 8 |
y | 5 | 8 | 12 | 14 | 16 |
其中![]() ,
,![]() ,
,![]() 是对当地GDP的增长贡献值.
是对当地GDP的增长贡献值.
(1)若从五组数据中任取两组,求至少有一组满足![]() 的概率;
的概率;
(2)对于表中数据,甲、乙两个同学给出的拟合直线方程为:![]() ,
,![]() ,试用最小二乘法判断哪条直线的拟合程度更好.(附:
,试用最小二乘法判断哪条直线的拟合程度更好.(附:![]() ;Q越小拟合度越好.)
;Q越小拟合度越好.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥P﹣ABC的所有棱长为1.M是底面△ABC内部一个动点(包括边界),且M到三个侧面PAB,PBC,PAC的距离h1,h2,h3成单调递增的等差数列,记PM与AB,BC,AC所成的角分别为α,β,γ,则下列正确的是( )
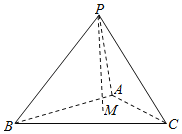
A.α=βB.β=γC.α<βD.β<γ
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,以极点为原点
,以极点为原点![]() ,极轴为
,极轴为![]() 轴正半轴(两坐标系取相同的单位长度)的直角坐标系
轴正半轴(两坐标系取相同的单位长度)的直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为:
的参数方程为:![]() 为参数).
为参数).
(1)求曲线![]() 的直角坐标方程与曲线
的直角坐标方程与曲线![]() 的普通方程;
的普通方程;
(2)将曲线![]() 经过伸缩变换
经过伸缩变换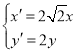 后得到曲线
后得到曲线![]() ,若
,若![]() ,
,![]() 分别是曲线
分别是曲线![]() 和曲线
和曲线![]() 上的动点,求
上的动点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]()
![]() 的离心率为
的离心率为![]() ,圆
,圆![]() 与
与![]() 轴正半轴交于点
轴正半轴交于点![]() ,圆
,圆![]() 在点
在点![]() 处的切线被椭圆
处的切线被椭圆![]() 截得的弦长为
截得的弦长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设圆![]() 上任意一点
上任意一点![]() 处的切线交椭圆
处的切线交椭圆![]() 于点
于点![]() ,
,![]() ,试判断
,试判断![]() 是否为定值?若为定值,求出该定值;若不是定值,请说明理由.
是否为定值?若为定值,求出该定值;若不是定值,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com