
【题目】已知函数f(x)=lnx+ax2(a∈R),y=f(x)的图象连续不间断.
(1)求函数y=f(x)的单调区间;
(2)当a=1时,设l是曲线y=f(x)的一条切线,切点是A,且l在点A处穿过函数y=f(x)的图象(即动点在点A附近沿曲线y=f(x)运动,经过点A时,从l的一侧进入另一侧),求切线l的方程.
【答案】
(1)解:函数的导数f′(x)= ![]() +2ax=
+2ax= ![]() (x>0),
(x>0),
若a≥0,则f'(x)>0,此时函数单调递增,即增区间为(0,+∞);
若a<0,由f′(x)>0,得2ax2+1>0,即 ![]() ,得0<x<
,得0<x< ![]() ,
,
由f′(x)<0,得x> ![]() .
.
∴函数的减区间为( ![]() ,+∞),增区间为(0,
,+∞),增区间为(0, ![]() ),
),
综上:若a≥0,函数的增区间为(0,+∞).
若a<0,函数的增区间为(0, ![]() ),减区间为(
),减区间为( ![]() ,+∞);
,+∞);
(2)设切点A(x0,f(x0)),x0>0, ![]() ,
,
∴在点A处切线的斜率是 ![]() .
.
∴切线方程为 ![]() ,
,
即 ![]() .
.
l在点A处穿过函数y=f(x)的图象,即在点A的两侧,曲线y=f(x)在直线的两侧,
令 ![]() ,设h(x)=f(x)﹣g(x),
,设h(x)=f(x)﹣g(x),
∴在x=x0附近两侧h(x)的值异号.
设 ![]() ﹣lnx0,注意到h(x0)=0.
﹣lnx0,注意到h(x0)=0.
下面研究函数的单调性:
![]() =
= ![]() =
= ![]() .
.
当 ![]() 时:
时:
x | (0,x0) | (x0, | ( |
h′(x) | + | ﹣ | + |
h(x) | 增 | 减 | 增 |
∴当x∈(0,x0)时,h(x)是增函数,则h(x)<h(x0)=0,
当x∈( ![]() ,+∞)时,h(x)是减函数,则h(x)<h(x0)=0.
,+∞)时,h(x)是减函数,则h(x)<h(x0)=0.
∴h(x)在x=x0处取极大值,两侧附近同负,与题设不符;
同理,当x0 ![]() 时,h(x)在x=x0处取极小值,两侧附近同正,与题设不符;
时,h(x)在x=x0处取极小值,两侧附近同正,与题设不符;
故 ![]() ,即
,即 ![]() 时,h′(x)=
时,h′(x)= ![]() ,∴h(x)在(0,+∞)内单调递增.
,∴h(x)在(0,+∞)内单调递增.
∴当x∈(0,x0)时,h(x)<h(x0)=0,当x∈( ![]() ,+∞),h(x)>h(x0)=0符合题设.
,+∞),h(x)>h(x0)=0符合题设.
∴ ![]() ,切线方程为
,切线方程为 ![]() .
.
【解析】(1)先对函数f(x)求导,再对a的值分情况判断函数f(x)的单调性,从而函数y=f(x)的单调区间;(2)先设切点A(x0,f(x0)),x0>0,进而利用导数求出函数f(x)在A处的切线方程,再由已知条件转化为在点A的两侧,曲线y=f(x)在直线的两侧,进而构造函数h(x)=f(x)﹣g(x),从而可得在x=x0附近两侧h(x)的值异号,最后利用导数研究函数h(x)单调性,进而可得x0,从而可得切线l的方程.
【考点精析】本题主要考查了利用导数研究函数的单调性的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减才能正确解答此题.
在这个区间单调递减才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】函数y=sin(ωx+φ)(x∈R,ω>0,0≤φ<2π)的部分图象如图,则函数表达式为;若将该函数向左平移1个单位,再保持纵坐标不变,横坐标缩短为原来的 ![]() 倍得到函数g(x)= .
倍得到函数g(x)= . 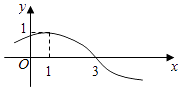
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了竖一块广告牌,要制造三角形支架,如图,要求∠ACB=60°,BC的长度大于1米,且AC比AB长0.5米,为了稳固广告牌,要求AC越短越好,则AC最短为( )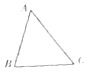
A.(1+ ![]() )米
)米
B.2米
C.(1+ ![]() )米
)米
D.(2+ ![]() )米
)米
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知极坐标系的极点在直角坐标系的原点,极轴与x轴的正半轴重合,曲线C的极坐标方程为ρ2cos2θ+3ρ2sin2θ=3,直线l的参数方程为 ![]() .试在曲线C上求一点M,使它到直线l的距离最大.
.试在曲线C上求一点M,使它到直线l的距离最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,
, ![]() .
.
(1)求函数f(x)的值域;
(2)已知锐角△ABC的两边长a,b分别为函数f(x)的最小值与最大值,且△ABC的外接圆半径为 ![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】集合L={l|l与直线y=x相交,且以交点的横坐标为斜率}.若直线l′∈L,点P(﹣1,2)到直线l′的最短距离为r,则以点P为圆心,r为半径的圆的标准方程为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记等差数列{an}的前n项和为Sn .
(1)求证:数列{ ![]() }是等差数列;
}是等差数列;
(2)若a1=1,对任意的n∈N*,n≥2,均有 ![]() ,
, ![]() ,
, ![]() 是公差为1的等差数列,求使
是公差为1的等差数列,求使 ![]() 为整数的正整数k的取值集合;
为整数的正整数k的取值集合;
(3)记bn=a ![]() (a>0),求证:
(a>0),求证: ![]() ≤
≤ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx+x2 .
(Ⅰ)若函数g(x)=f(x)﹣ax在其定义域内为增函数,求实数a的取值范围;
(Ⅱ)在(Ⅰ)的条件下,若a>1,h(x)=e3x﹣3aexx∈[0,ln2],求h(x)的极小值;
(Ⅲ)设F(x)=2f(x)﹣3x2﹣kx(k∈R),若函数F(x)存在两个零点m,n(0<m<n),且2x0=m+n.问:函数F(x)在点(x0 , F(x0))处的切线能否平行于x轴?若能,求出该切线方程;若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=﹣x3+x2(x∈R),g(x)满足g′(x)= ![]() (a∈R,x>0),且g(e)=a,e为自然对数的底数.
(a∈R,x>0),且g(e)=a,e为自然对数的底数.
(Ⅰ)已知h(x)=e1﹣xf(x),求h(x)在(1,h(1))处的切线方程;
(Ⅱ)若存在x∈[1,e],使得g(x)≥﹣x2+(a+2)x成立,求a的取值范围;
(Ⅲ)设函数F(x)= ![]() ,O为坐标原点,若对于y=F(x)在x≤﹣1时的图象上的任一点P,在曲线y=F(x)(x∈R)上总存在一点Q,使得
,O为坐标原点,若对于y=F(x)在x≤﹣1时的图象上的任一点P,在曲线y=F(x)(x∈R)上总存在一点Q,使得 ![]()
![]() <0,且PQ的中点在y轴上,求a的取值范围.
<0,且PQ的中点在y轴上,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com