
【题目】如图,在等腰梯形ABCD中,AD∥BC,AB=BC=CD=1,AD=2,点E、F分别在线段AB、AD上,且EF∥CD,将△AEF沿EF折起到△MEF的位置,并使平面MEF⊥平面BCDFE,得到几何体M﹣BCDEF,则折叠后的几何体的体积的最大值为_____.
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
【题目】某市场研究人员为了了解产业园引进的甲公司前期的经营状况,对该公司2018年连续六个月的利润进行了统计,并根据得到的数据绘制了相应的折线图,如图所示
(1)由折线图可以看出,可用线性回归模型拟合月利润![]() (单位:百万元)与月份代码
(单位:百万元)与月份代码![]() 之间的关系,求
之间的关系,求![]() 关于
关于![]() 的线性回归方程,并预测该公司2019年3月份的利润;
的线性回归方程,并预测该公司2019年3月份的利润;
(2)甲公司新研制了一款产品,需要采购一批新型材料,现有![]() ,
,![]() 两种型号的新型材料可供选择,按规定每种新型材料最多可使用
两种型号的新型材料可供选择,按规定每种新型材料最多可使用![]() 个月,但新材料的不稳定性会导致材料损坏的年限不相同,现对
个月,但新材料的不稳定性会导致材料损坏的年限不相同,现对![]() ,
,![]() 两种型号的新型材料对应的产品各
两种型号的新型材料对应的产品各![]() 件进行科学模拟测试,得到两种新型材料使用寿命的频数统计如下表:
件进行科学模拟测试,得到两种新型材料使用寿命的频数统计如下表:
使用寿命 材料类型 |
|
|
|
| 总计 |
|
|
|
|
|
|
|
|
|
|
|
|
如果你是甲公司的负责人,你会选择采购哪款新型材料?
参考数据:![]() ,
,![]() .参考公式:回归直线方程为
.参考公式:回归直线方程为![]() ,其中
,其中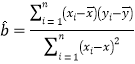
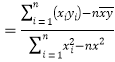 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
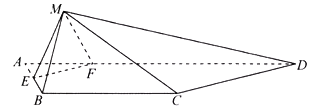
【题目】如图1所示,在等腰梯形ABCD中,![]() ,
,![]() ,垂足为E,
,垂足为E,![]() ,
,![]() 将
将![]() 沿EC折起到
沿EC折起到![]() 的位置,如图2所示,使平面
的位置,如图2所示,使平面![]() 平面ABCE.
平面ABCE.
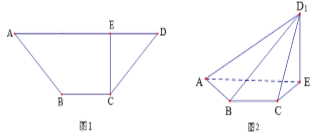
(1)连结BE,证明:![]() 平面
平面![]() ;
;
(2)在棱![]() 上是否存在点G,使得
上是否存在点G,使得![]() 平面
平面![]() ,若存在,直接指出点G的位置
,若存在,直接指出点G的位置![]() 不必说明理由
不必说明理由![]() ,并求出此时三棱锥
,并求出此时三棱锥![]() 的体积;若不存在,请说明理由.
的体积;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣2mx﹣n(0<x<1),其中m,n∈R,e为自然对数的底数.
(1)试讨论函数f(x)的极值;
(2)记函数g(x)=ex﹣mx2﹣nx﹣1(0<x<1),且g(x)的图象在点![]() 处的切的斜率为
处的切的斜率为![]() ,若函数g(x)存在零点,试求实数m的取值范围.
,若函数g(x)存在零点,试求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中曲线
中曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,直线
轴的正半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程以及直线
的普通方程以及直线![]() 的直角坐标方程;
的直角坐标方程;
(2)将曲线![]() 向左平移2个单位,再将曲线
向左平移2个单位,再将曲线![]() 上的所有点的横坐标缩短为原来的
上的所有点的横坐标缩短为原来的![]() ,得到曲线
,得到曲线![]() ,求曲线
,求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣1|+|2x﹣6|(x∈R),记f(x)的最小值为c.
(1)求c的值;
(2)若实数ab满足a>0,b>0,a+b=c,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com