
某分公司经销某种品牌产品,每件产品的成本为3元,并且每件产品需向总公司交a元(3≤a≤5)的管理费,预计当每件产品的售价为x元(9≤x≤11)时,一年的销售量为(12-x)2万件.
(1)求分公司一年的利润L(万元)与每件产品的售价x的函数关系式;
(2)当每件产品的售价为多少元时,分公司一年的利润L最大?并求出L的最大值Q(a).
(1)L=(x-3-a)·(12-x)2,x∈[9,11].(2)当每件售价为6+ a元时,分公司一年的利润L最大,最大值Q(a)=4
a元时,分公司一年的利润L最大,最大值Q(a)=4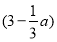 3(万元).
3(万元).
【解析】(1)分公司一年的利润L(万元)与售价x的函数关系式为L=(x-3-a)·(12-x)2,x∈[9,11].
(2)L′(x)=(12-x)2-2(x-3-a)(12-x)=(12-x)·(18+2a-3x).
令L′=0,得x=6+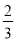 a或x=12(不合题意,舍去).
a或x=12(不合题意,舍去).
∵3≤a≤5,∴8≤6+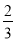 a≤
a≤ .
.
在x=6+ a两侧,L′的值由正变负.
a两侧,L′的值由正变负.
所以①当8≤6+ a<9,即3≤a<
a<9,即3≤a<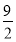 时,
时,
Lmax=L(9)=(9-3-a)(12-9)2=9(6-a);
②当9≤6+ a≤
a≤ ,即
,即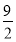 ≤a≤5时,
≤a≤5时,
Lmax=L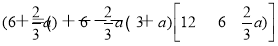 2=4
2=4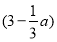 3,
3,
所以Q(a)=
故若3≤a<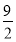 ,则当每件售价为9元时,分公司一年的利润L最大,最大值Q(a)=9(6-a)(万元);若
,则当每件售价为9元时,分公司一年的利润L最大,最大值Q(a)=9(6-a)(万元);若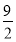 ≤a≤5,则当每件售价为6+
≤a≤5,则当每件售价为6+ a元时,分公司一年的利润L最大,最大值Q(a)=4
a元时,分公司一年的利润L最大,最大值Q(a)=4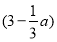 3(万元).
3(万元).


科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷1练习卷(解析版) 题型:选择题
记△ABC各边的中点分别为D,E,F,在A,B,C,D,E,F中任取4点,若这4点为平行四边形顶点,则称为选取成功.某人连续进行3次这种选取,则至少成功1次的概率是( ).
A.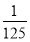 B.
B.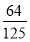 C.
C.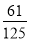 D.
D.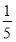
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练5练习卷(解析版) 题型:填空题
关于x的方程x3-3x2-a=0有三个不同的实数解,则实数a的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练3练习卷(解析版) 题型:解答题
已知函数f(x)=x2+bx+c(b,c∈R),对任意的x∈R,恒有f′(x)≤f(x).
(1)证明:当x≥0时,f(x)≤(x+c)2;
(2)若对满足题设条件的任意b,c,不等式f(c)-f(b)≤M(c2-b2)恒成立,求M的最小值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练3练习卷(解析版) 题型:选择题
在平面直角坐标系xOy中,M为不等式组 所表示的区域上一动点,则直线OM斜率的最小值为( ).
所表示的区域上一动点,则直线OM斜率的最小值为( ).

A.2 B.1 C.-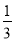 D.-
D.-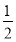
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练2练习卷(解析版) 题型:选择题
若函数y=f(x)(x∈R)满足f(x+1)=-f(x),且x∈[-1,1]时f(x)=1-x2.函数g(x)= 则函数h(x)=f(x)-g(x)在区间[-5,4]内的零点的个数( ).
则函数h(x)=f(x)-g(x)在区间[-5,4]内的零点的个数( ).
A.7 B.8?,
C.9 D.10
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练1练习卷(解析版) 题型:解答题
已知函数f(x)=loga(x+1)(a>1),若函数y=g(x)的图象上任意一点P关于原点对称的点Q的轨迹恰好是函数f(x)的图象.
(1)写出函数g(x)的解析式;
(2)当x∈[0,1)时总有f(x)+g(x)≥m成立,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习7-2随机变量及其分布练习卷(解析版) 题型:选择题
若随机变量X的概率分布密度函数是φμ,σ(x)= (x∈R),则E(2X-1)=( ).
(x∈R),则E(2X-1)=( ).
A.-1 B.-2
C.-4 D.-5
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习4-2数列求和与数列的综合应用练习卷(解析版) 题型:解答题
已知Sn是数列{an}的前n项和,且an=Sn-1+2(n≥2),a1=2.
(1)求数列{an}的通项公式.
(2)设bn=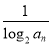 ,Tn=bn+1+bn+2+…+b2n,是否存在最大的正整数k,使得
,Tn=bn+1+bn+2+…+b2n,是否存在最大的正整数k,使得
对于任意的正整数n,有Tn>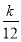 恒成立?若存在,求出k的值;若不存在,说明理由.
恒成立?若存在,求出k的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com