
【题目】已知函数f(x)=Acos( ![]() +
+ ![]() ),x∈R,且f(
),x∈R,且f( ![]() )=
)= ![]() .
.
(1)求A的值;
(2)设α,β∈[0, ![]() ],f(4α+
],f(4α+ ![]() π)=﹣
π)=﹣ ![]() ,f(4β﹣
,f(4β﹣ ![]() π)=
π)= ![]() ,求cos(α+β)的值.
,求cos(α+β)的值.
【答案】
(1)解:对于函数f(x)=Acos( ![]() +
+ ![]() ),x∈R,由f(
),x∈R,由f( ![]() )=Acos
)=Acos ![]() =
= ![]() A=
A= ![]() ,
,
可得A=2
(2)解:由于α,β∈[0, ![]() ],f(4α+
],f(4α+ ![]() π)=2cos(
π)=2cos( ![]() +
+ ![]() )=2cos(α+
)=2cos(α+ ![]() )=﹣2sinα=﹣
)=﹣2sinα=﹣ ![]() ,
,
∴sinα= ![]() ,∴cosα=
,∴cosα= ![]() =
= ![]() .
.
又 f(4β﹣ ![]() π)=2cos(
π)=2cos( ![]() +
+ ![]() )=2cosβ=
)=2cosβ= ![]() ,∴cosβ=
,∴cosβ= ![]() ,∴sinβ=
,∴sinβ= ![]() =
= ![]() .
.
∴cos(α+β)=cosαcosβ﹣sinαsinβ= ![]() ×
× ![]() ﹣
﹣ ![]() ×
× ![]() =
= ![]()
【解析】(1)直接利用条件求得A的值.(2)由条件根据f(4α+ ![]() π)=﹣
π)=﹣ ![]() ,求得sinα的值,再利用同角三角函数的基本关系求得cosα的值;由f(4β﹣
,求得sinα的值,再利用同角三角函数的基本关系求得cosα的值;由f(4β﹣ ![]() π)=
π)= ![]() ,求得cosβ的值,再利用同角三角函数的基本关系求得sinβ的值;从而求得cos(α+β)=cosαcosβ﹣sinαsinβ的值.
,求得cosβ的值,再利用同角三角函数的基本关系求得sinβ的值;从而求得cos(α+β)=cosαcosβ﹣sinαsinβ的值.
【考点精析】利用两角和与差的余弦公式对题目进行判断即可得到答案,需要熟知两角和与差的余弦公式:![]() .
.


科目:高中数学 来源: 题型:
【题目】为了解学生寒假期间学习情况,学校对某班男、女学生学习时间进行调查,学习时间按整小时统计,调查结果绘成折线图如下:
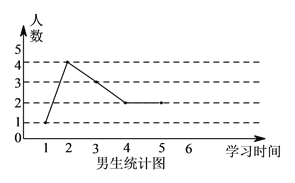
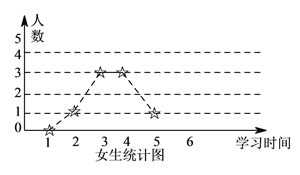
(I)已知该校有![]() 名学生,试估计全校学生中,每天学习不足
名学生,试估计全校学生中,每天学习不足![]() 小时的人数.
小时的人数.
(II)若从学习时间不少于![]() 小时的学生中选取
小时的学生中选取![]() 人,设选到的男生人数为
人,设选到的男生人数为![]() ,求随机变量
,求随机变量![]() 的分布列.
的分布列.
(III)试比较男生学习时间的方差![]() 与女生学习时间方差
与女生学习时间方差![]() 的大小.(只需写出结论).
的大小.(只需写出结论).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某旅游区拟建一主题游乐园,该游乐区为五边形区域ABCDE,其中三角形区域ABE为主题游乐区,四边形区域为BCDE为休闲游乐区,AB、BC,CD,DE,EA,BE为游乐园的主要道路(不考虑宽度).![]()
![]() .
.

(I)求道路BE的长度;
(Ⅱ)求道路AB,AE长度之和的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对定义域分别为D1 , D2的函数y=f(x),y=g(x),规定:函数h(x)= 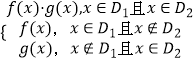 ,f(x)=x﹣2(x≥1),g(x)=﹣2x+3(x≤2),则h(x)的单调减区间是 .
,f(x)=x﹣2(x≥1),g(x)=﹣2x+3(x≤2),则h(x)的单调减区间是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com