Question

【题目】已知函数 f(x)＝，x∈R，其中 a＞0.

(Ⅰ)求函数 f(x)的单调区间；

(Ⅱ)若函数 f(x)（x∈(－2,0)）的图象与直线 y=a 有两个不同交点，求 a 的取值范围．

Answer 1

【答案】（1）函数 f(x)的单调递增区间是(－∞，－1)，(a，＋∞)；单调递减区间是(－1，a)．

（2）(0, ).

【解析】

分析：（1）先求函数的导函数，找出导函数的零点，把定义域由零点分成几个区间判断导函数在各区间内的符号，从而得到原函数在个区间内的单调性；（2）根据（1）中求出的单调区间，说明函数在区间（-2，-1）内单调递增，在区间（-1，0）内单调递减，结合函数零点和方程根的转化列式可求a的范围．

详解：

(Ⅰ)f′(x)＝＋(1－a)x－a＝(x＋1)(x－a)．

由 f′(x)＝0，得＝－1，＝a＞0.

当 x 变化时，f′(x)，f(x)的变化情况如下表：

x	(－∞，－1)	－1	(－1，a)	a	(a，＋∞)
f′(x)	＋	0	－	0	＋
f(x)		极大值		极小值

故函数 f(x)的单调递增区间是(－∞，－1)，(a，＋∞)；

单调递减区间是(－1，a)．

(Ⅱ) 令 g(x)=f(x)-a，x∈(－2,0)，

则函数 g(x)在区间(－2,0)内有两个不同的零点，

由(Ⅰ)知 g (x)在区间(－2，－1)内单调递增，在区间(－1，0)内单调递减，

从而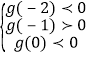

解得 0＜a＜. 所以 a 的取值范围是(0, )