
【题目】判断下列命题是全称命题还是特称命题,并判断其真假;写出这些命题的否定并判断真假.
(1)三角形的内角和为180°;
(2)每个二次函数的图象都开口向下;
(3)存在一个四边形不是平行四边形;
(4)![]() ;
;
(5).![]()
【答案】
(1)
【解答】
解:是全称命题且为真命题.
命题的否定:三角形的内角和不全为180°,
即存在一个三角形,它的内角和不等于180°,为假命题.
(2)
【解答】
解:是全称命题且为假命题.
命题的否定:存在一个二次函数的图象开口不向下,为真命题.
(3)
【解答】
解:是特称命题且为真命题.
命题的否定:所有的四边形都是平行四边形,为假命题.
(4)
【解答】
解:是全称命题且为真命题.
由于 ![]() 都有
都有 ![]() ,故
,故 ![]() , p 为真命题;
, p 为真命题;
![]() :
: ![]() ,
, ![]() 为假命题
为假命题
(5)
【解答】
解:是特称命题且为假命题.
因为不存在一个实数 x ,使 ![]() 成立, p 为假命题;
成立, p 为假命题;
![]() :
: ![]() ,
, ![]() 为真命题.
为真命题.
【解析】命题的否定要与否命题区别开来,全称命题的否定是特称命题,而特称命题的否定是全称命题.
【考点精析】解答此题的关键在于理解全称命题的相关知识,掌握全称命题![]() :
:![]() ,
,![]() ,它的否定
,它的否定![]() :
:![]() ,
,![]() ;全称命题的否定是特称命题.
;全称命题的否定是特称命题.


 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源: 题型:
【题目】如图,M,N,K分别是正方体ABCD﹣A1B1C1D1的棱AB,CD,C1D1的中点. 
(1)求证:AN∥平面A1MK;
(2)求证:平面A1B1C⊥平面A1MK.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C1: ![]() (a>b>0)的离心率为e=
(a>b>0)的离心率为e=![]() ,过C1的左焦点F1的直线l:x-y+2=0,直线l被圆C2:
,过C1的左焦点F1的直线l:x-y+2=0,直线l被圆C2: ![]() +
+![]() =
=![]() (r>0)截得的弦长为2
(r>0)截得的弦长为2![]() .
.
(1)求椭圆C1的方程:
(2)设C1的右焦点为F2,在圆C2上是否存在点P,满足|PF1|=![]() |PF2|,若存在,指出有几个这样的点(不必求出点的坐标);若不存在,说明理由.
|PF2|,若存在,指出有几个这样的点(不必求出点的坐标);若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:函数f(x)=lg(ax2-x+ ![]() a)的定义域为R;命题q:不等式3x-9x<a对一切正实数均成立.如果命题“p∨q”为真命题,“p∧q”为假命题,求实数a的取值范围( ).
a)的定义域为R;命题q:不等式3x-9x<a对一切正实数均成立.如果命题“p∨q”为真命题,“p∧q”为假命题,求实数a的取值范围( ).
A.0≤a<1
B.0≤a
C.a≤1
D.0≤a≤1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了得到函数y=sin(x+ ![]() )的图象,只需把y=sinx图象上所有的点( )
)的图象,只需把y=sinx图象上所有的点( )
A.向左平移 ![]() 个单位
个单位
B.向右平移 ![]() 个单位
个单位
C.向左平移 ![]() 个单位
个单位
D.向右平移 ![]() 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂为了对新研发的一种产品进行合理定价,随机抽取了6个试销售数据,得到第i个销售单价xi(单位:元)与销售yi(单位:件)的数据资料,算得 ![]()
(1)求回归直线方程 ![]() ;
;
(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入﹣成本) 附:回归直线方程 ![]() 中,
中, ![]() =
= 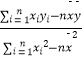 ,
, ![]() =
= ![]() ﹣
﹣ ![]() ,其中
,其中 ![]() ,
, ![]() 是样本平均值.
是样本平均值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com