
【题目】如图,四棱锥![]() 中,
中,![]() ,且
,且![]() .
.
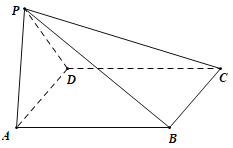
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() 是等边三角形,
是等边三角形,![]() ,且四棱锥
,且四棱锥![]() 的体积为
的体积为![]() ,求
,求![]() 的面积.
的面积.
科目:高中数学 来源: 题型:
【题目】如图所示的五个区域中,中心区![]() 域是一幅图画,现要求在其余四个区域中涂色,有四种颜色可供选择.要求每个区域只涂一种颜色且相邻区域所涂颜色不同,则不同的涂色方法种数为( )
域是一幅图画,现要求在其余四个区域中涂色,有四种颜色可供选择.要求每个区域只涂一种颜色且相邻区域所涂颜色不同,则不同的涂色方法种数为( )

A. 56 B. 72 C. 64 D. 84
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】时下,网校教学越来越受到广大学生的喜爱,它已经成为学生们课外学习的一种趋势,假设某网校的套题每日的销售量![]() (单位:千套)与销售价格
(单位:千套)与销售价格![]() (单位:元/套)满足的关系式
(单位:元/套)满足的关系式![]() ,其中
,其中![]() ,
,![]() 为常数.已知销售价格为4元/套时,每日可售出套题21千套.
为常数.已知销售价格为4元/套时,每日可售出套题21千套.
(1)求![]() 的值;
的值;
(2)假设网校的员工工资,办公等所有开销折合为每套题2元(只考虑销售出的套数),试确定销售价格![]() 的值,使网校每日销售套题所获得的利润最大.(保留1位小数)
的值,使网校每日销售套题所获得的利润最大.(保留1位小数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com