
【题目】已知函数f(x)=![]()
(1)证明f(x)是奇函数;
(2)判断f(x)的单调性,并用定义证明
(3)求f(x)在[1,2]上的最值.
【答案】解:(1)由于函数f(x)=![]() 的定义域为R,f(﹣x)=
的定义域为R,f(﹣x)=![]() =
=![]() =﹣f(x),
=﹣f(x),
故函数f(x)为奇函数.
(2)由于f(x)=![]() =
=![]() =1﹣
=1﹣![]() ,设x1<x2 , 则
,设x1<x2 , 则![]() <
<![]() ,
,
根据f(x1)﹣f(x2)=[1﹣![]() ]﹣[1﹣
]﹣[1﹣![]() ]=
]=![]() ﹣
﹣![]()
=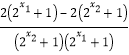 =
=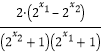 <0,∴f(x1)<f(x2),
<0,∴f(x1)<f(x2),
故函数f(x)在R上为增函数.
(3)在[1,2]上,函数f(x)为增函数,故当x=1时,函数f(x)取得最小值为![]() ,
,
当x=2时,函数f(x)取得最大值为![]() .
.
【解析】(1)由条件利用奇函数的定义进行判断,可得结论.
(2)由条件利用函数的单调性的定义进行证明,可得结论.
(3)由条件利用函数的单调性求得f(x)在[1,2]上的最值.
【考点精析】解答此题的关键在于理解奇偶性与单调性的综合的相关知识,掌握奇函数在关于原点对称的区间上有相同的单调性;偶函数在关于原点对称的区间上有相反的单调性,以及对三角函数的最值的理解,了解函数![]() ,当
,当![]() 时,取得最小值为
时,取得最小值为![]() ;当
;当![]() 时,取得最大值为
时,取得最大值为![]() ,则
,则![]() ,
,![]() ,
,![]() .
.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
【题目】某蛋糕店每天做若干个生日蛋糕,每个制作成本为50元,当天以每个100元售出,若当天白天售不出,则当晚以30元/个价格作普通蛋糕低价售出,可以全部售完.
(1)若蛋糕店每天做20个生日蛋糕,求当天的利润![]() (单位:元)关于当天生日蛋糕的需求量
(单位:元)关于当天生日蛋糕的需求量![]() (单位:个,
(单位:个, ![]() )的函数关系;
)的函数关系;
(2)蛋糕店记录了100天生日蛋糕的日需求量(单位:个)整理得下表:

(ⅰ)假设蛋糕店在这100天内每天制作20个生日蛋糕,求这100天的日利润(单位:元)的平均数;
(ⅱ)若蛋糕店一天制作20个生日蛋糕,以100天记录的各需求量的频率作为概率,求当天利润不少于900元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果数据x1 , x2 , …,xn的平均数是 ![]() ,方差是S2 , 则2x1+3,2x2+3,…,2xn+3的平均数和方差分别是( )
,方差是S2 , 则2x1+3,2x2+3,…,2xn+3的平均数和方差分别是( )
A.![]() 和S
和S
B.2 ![]() +3和4S2
+3和4S2
C.![]() 和S2
和S2
D.![]() 和4S2+12S+9
和4S2+12S+9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标平面中, ![]() 的两个顶点为
的两个顶点为![]() ,平面内两点
,平面内两点![]() 、
、![]() 同时满足:①
同时满足:①![]() ;②
;②![]() ;③
;③![]() .
.
(1)求顶点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 作两条互相垂直的直线
作两条互相垂直的直线![]() ,直线
,直线![]() 与点
与点![]() 的轨迹
的轨迹![]() 相交弦分别为
相交弦分别为![]() ,设弦
,设弦![]() 的中点分别为
的中点分别为![]() .
.
①求四边形![]() 的面积
的面积![]() 的最小值;
的最小值;
②试问:直线![]() 是否恒过一个定点?若过定点,请求出该定点,若不过定点,请说明理由.
是否恒过一个定点?若过定点,请求出该定点,若不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2﹣2x+4my+4m2=0,圆C1:x2+y2=25,以及直线l:3x﹣4y﹣15=0.
(1)求圆C1:x2+y2=25被直线l截得的弦长;
(2)当m为何值时,圆C与圆C1的公共弦平行于直线l;
(3)是否存在m,使得圆C被直线l所截的弦AB中点到点P(2,0)距离等于弦AB长度的一半?若存在,求圆C的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的方程为
的方程为![]() ,点
,点![]() 是抛物线
是抛物线![]() 上到直线
上到直线![]() 距离最小的点,点
距离最小的点,点![]() 是抛物线上异于点
是抛物线上异于点![]() 的点,直线
的点,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,过点
,过点![]() 与
与![]() 轴平行的直线与抛物线
轴平行的直线与抛物线![]() 交于点
交于点![]() .
.
(Ⅰ)求点![]() 的坐标;
的坐标;
(Ⅱ)证明直线![]() 恒过定点,并求这个定点的坐标.
恒过定点,并求这个定点的坐标.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知全集U=R,集合A={x|x![]()
![]() },集合B={x|x≤1},那么U(A∩B)等于( )
},集合B={x|x≤1},那么U(A∩B)等于( )
A.{x|x![]()
![]() 或x>1}
或x>1}
B.{x|![]()
![]() x
x![]() 1}
1}
C.{x|x≤![]() 或x
或x![]() 1}
1}
D.{x|![]() ≤x≤1}
≤x≤1}
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com