
【题目】△ABC的三角A,B,C的对边分别为a,b,c满足(2b﹣c)cosA=acosC.
(1)求A的值;
(2)若a=2,求△ABC面积的最大值;
(3)若a=2,求△ABC周长的取值范围.
【答案】
(1)解:将(2b﹣c)cosA=acosC代入正弦定理得:
(2sinB﹣sinC)cosA=sinAcosC,
即2sinBcosA=sinCcosA+cosCsinA=sin(A+C)=sinB,
由B∈(0,180°),得到sinB≠0,
所以cosA= ![]() ,又A∈(0,180°),
,又A∈(0,180°),
则A的度数为60°
(2)解:∵a=2,A=60°,
∴由余弦定理a2=b2+c2﹣2bccosA,得
4=b2+c2﹣2bccos60°,即b2+c2﹣bc=4
∴b2+c2=4+bc≥2bc,可得bc≤4
又∵△ABC的面积S= ![]() bcsinA=
bcsinA= ![]() bc≤
bc≤ ![]()
∴当且仅当b=c=2时,△ABC的面积的最大值为 ![]() ,此时△ABC是等边三角形
,此时△ABC是等边三角形
(3)解:由题意,b>0,c>0,b+c>a=2,
∴由余弦定理4=b2+c2﹣2bccos60°=(b+c)2﹣3bc≥ ![]() (b+c)2(当且仅当b=c时取等号),
(b+c)2(当且仅当b=c时取等号),
∴b+c≤4,
∵b+c>2,
∴2<b+c≤4,
∴△ABC的周长的取值范围为(4,6]
【解析】(1)利用正弦定理化简已知的等式,再利用两角和的正弦函数公式及诱导公式化简,根据sinB不为0,得到cosA的值,由A的范围,利用特殊角的三角函数值即可求出A的度数.(2)由余弦定理a2=b2+c2﹣2bccosA的式子,得到b2+c2﹣bc=4,结合基本不等式求出bc≤4,再用正弦定理的面积公式算出当且仅当b=c=2时,△ABC的面积的最大值为 ![]() .(3)利用余弦定理结合基本不等式,可求△ABC的周长的取值范围.
.(3)利用余弦定理结合基本不等式,可求△ABC的周长的取值范围.
【考点精析】根据题目的已知条件,利用正弦定理的定义的相关知识可以得到问题的答案,需要掌握正弦定理:![]() .
.


科目:高中数学 来源: 题型:
【题目】已知定理:“实数m,n为常数,若函数h(x)满足h(m+x)+h(m﹣x)=2n,则函数y=h(x)的图象关于点(m,n)成中心对称”.
(1)已知函数f(x)= ![]() 的图象关于点(1,b)成中心对称,求实数b的值;
的图象关于点(1,b)成中心对称,求实数b的值;
(2)已知函数g(x)满足g(2+x)+g(﹣x)=4,当x∈[0,2]时,都有g(x)≤3成立,且当x∈[0,1]时,g(x)=2k(x﹣1)+1 , 求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:y=ax+1﹣a(a∈R).若存在实数a使得一条曲线与直线l有两个不同的交点,且以这两个交点为端点的线段长度恰好等于|a|,则称此曲线为直线l的“绝对曲线”.下面给出四条曲线方程:①y=﹣2|x﹣1|;②y=x2;③(x﹣1)2+(y﹣1)2=1;④x2+3y2=4;则其中直线l的“绝对曲线”有( )
A.①④
B.②③
C.②④
D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商店计划每天购进某商品若干件,商店每销售1件该商品可获利50元.若供大于求,剩余商品全部退回,则每件商品亏损10元;若供不应求,则从外部调剂,此时每件调剂商品可获利30元.
(Ⅰ)若商店一天购进该商品10件,求当天的利润y(单位:元)关于当天需求量n(单位:件,n∈N)的函数解析式;
(Ⅱ)商店记录了50天该商品的日需求量(单位:件),整理得下表:
日需求量n | 8 | 9 | 10 | 11 | 12 |
频数 | 10 | 10 | 15 | 10 | 5 |
①假设该店在这50天内每天购进10件该商品,求这50天的日利润(单位:元)的平均数;
②若该店一天购进10件该商品,记“当天的利润在区间![]() ”为事件A,求P(A)的估计值.
”为事件A,求P(A)的估计值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某单位员工的月工资水平,从该单位500位员工中随机抽取了50位进行调查,得到如下频数分布表和频率分布直方图:
月工资 | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
男员工数 | 1 | 8 | 10 | 6 | 4 | 4 |
女员工数 | 4 | 2 | 5 | 4 | 1 | 1 |

(1)试由图估计该单位员工月平均工资;
(2)现用分层抽样的方法从月工资在[45,55)和[55,65)的两组所调查的男员工中随机选取5人,问各应抽取多少人?
(3)若从月工资在[25,35)和[45,55)两组所调查的女员工中随机选取2人,试求这2人月工资差不超过1000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}中,a1=1,an+1=2an+1 (I)求证数列{an+1}是等比数列;
(II)设cn=n(an+1),求数列{cn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某生态公园的平面图呈长方形(如图),已知生态公园的长AB=8(km),宽AD=4(km),M,N分别为长方形ABCD边AD,DC的中点,P,Q为长方形ABCD边AB,BC(不含端点)上的一点.现公园管理处拟修建观光车道P﹣Q﹣N﹣M﹣P,要求观光车道围成四边形(如图阴影部分)的面积为15(km2),设BP=x(km),BQ=y(km), 
(1)试写出y关于x的函数关系式,并求出x的取值范围;
(2)若B为公园入口,P,Q为观光车站,观光车站P位于线段AB靠近入口B的一侧.经测算,每天由B入口至观光车站P,Q乘坐观光车的游客数量相等,均为1万人,问如何确定观光车站P,Q的位置,使所有游客步行距离之和最大,并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在圆内接△ABC,A,B,C所对的边分别为a,b,c,满足acosC+ccosA=2bcosB. 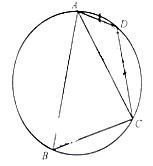
(1)求B的大小;
(2)若点D是劣弧 ![]() 上一点,AB=3,BC=2,AD=1,求四边形ABCD的面积.
上一点,AB=3,BC=2,AD=1,求四边形ABCD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com