练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知：函数（其中常数）.

    （Ⅰ）求函数的定义域及单调区间；

    （Ⅱ）若存在实数，使得不等式成立，求a的取值范围

    【答案】(1)的单调递增区间为，单调递减区间为，

    (2)

    【解析】

    （1）函数的定义域为………………………………………………1分

    ……………………………………………3分

    由，解得，由，解得且

    的单调递增区间为，单调递减区间为和………5分

    （2）由题意可知，当且仅当，且在上的最小值小于或等于时，存在实数，使得不等式成立 …………………………………6分

    若即时







    0

    +


    单减

    极小值

    单增

    在上的最小值为，则，得………9分

    若，即时，在上单调递减，则在上的最小值为，由，得（舍） ………………………………………11分

    综上所述，……………………………………………………………………12分

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知椭圆：的左、右焦点分别为，，过且垂直于轴的焦点弦的弦长为，过的直线交椭圆于，两点，且的周长为.

    （1）求椭圆的方程；

    （2）已知直线，互相垂直，直线过且与椭圆交于点，两点，直线过且与椭圆交于，两点.求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    (1)求函数的单调区间；

    (2)若不等式时恒成立，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥中，底面是平行四边形，，，且底面.

    (1)证明：平面平面；

    (2)若二面角为，求与平面所成角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某省的一个气象站观测点在连续4天里记录的AQI指数M与当天的空气水平可见度（单位：cm）的情况如表1：

    900

    700

    300

    100

    0.5

    3.5

    6.5

    9.5

    该省某市2017年11月份AQI指数频数分布如表2：

    频数（天）

    3

    6

    12

    6

    3

    <>（1）设，若与之间是线性关系，试根据表1的数据求出关于的线性回归方程；

    （2）小李在该市开了一家洗车店，洗车店每天的平均收入与AQI指数存在相关关系如表3：

    日均收入（元）

    -2000

    -1000

    2000

    6000

    8000

    根据表3估计小李的洗车店2017年11月份每天的平均收入.

    附参考公式：，其中，.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，直线的参数方程为（为参数），以坐标原点为极点，x轴正半轴为极轴建立极坐标系，曲线的极坐标方程为.

    （1）求直线的普通方程与曲线的直角坐标方程；

    （2）若直线与曲线交于两点，且设定点，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在等腰直角三角形中，，点是边上异于的一点，光线从点出发，经反射后又回到原点，光线经过的重心.

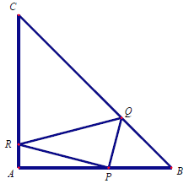
    （1）建立适当的坐标系，请求的重心的坐标；

    （2）求点的坐标；

    （3）求的周长及面积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（1）某校夏令营有3名男同学A、B、C和3名女同学X、Y、Z，其年级情况如下表：

    一年级

    二年级

    三年级

    男同学

    A

    B

    C

    女同学

    X

    Y

    Z

    现从这6名同学中随机选出2人参加知识竞赛(每人被选到的可能性相同)．

    ①用表中字母列举出所有可能的结果；

    ②设M为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”，求事件M发生的概率．

    （2）节日前夕，小李在家门前的树上挂了两串彩灯．这两串彩灯的第一次闪亮相互独立，且都在通电后的4秒内任一时刻等可能发生，然后每串彩灯以4秒为间隔闪亮．那么这两串彩灯同时通电后，它们第一次闪亮的时刻相差不超过2秒的概率是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设某地区乡居民人民币储蓄存款（年底余额）如下表：

    年份

    2012

    2013

    2014

    2015

    2016

    2017

    时间代号x

    1

    2

    3

    4

    5

    6

    储蓄存款y（千亿元）

    3.5

    5

    6

    7

    8

    9.5

    （1）求关于x的回归方程，并预测该地区2019年的人民币储蓄存款（用最简分数作答）.

    （2）在含有一个解释变量的线性模型中，恰好等于相关系数r的平方，当时，认为线性冋归模型是有效的，请计算并且评价模型的拟合效果（计算结果精确到0.001）.

    附：

    ，

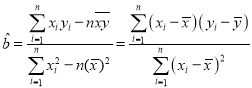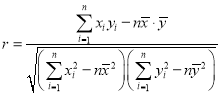
    查看答案和解析>>

    同步练习册答案