
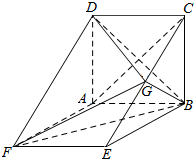
 如图,ABCD是边长为3的正方形,ABEF是矩形,平面ABCD上平面ABEF,G为EC的中点.
如图,ABCD是边长为3的正方形,ABEF是矩形,平面ABCD上平面ABEF,G为EC的中点.分析 (1)连接AE,交BF于O,由中位线定理可得OG∥AC,再由线面平行的判定得答案;
(2)由题意可知平面BCE⊥平面ABE,再由三棱锥C-DGB的体积为$\frac{9}{4}$求得BE,过G作GH⊥BE=H,过H作HK⊥BF于K,连接GK,则∠GKH为二面角E-BF-G的平面角.然后通过
解直角三角形得答案.
解答 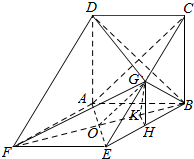 (1)证明:如图,
(1)证明:如图,
连接AE,交BF于O,∵ABEF是矩形,∴O为AE的中点,
连接OG,又G为EC的中点,∴OG∥AC,
∵OG?BGF,AC?BGF,
∴AC∥平面BFG;
(2)解:∵ABCD是边长为3的正方形,∴${S}_{△BCD}=\frac{9}{2}$,
又G到平面BCD的距离为$\frac{BE}{2}$,
∴${V}_{C-DGB}={V}_{G-BCD}=\frac{1}{3}×\frac{9}{2}×\frac{BE}{2}=\frac{9}{4}$,则BE=3.
过G作GH⊥BE=H,过H作HK⊥BF于K,连接GK,则∠GKH为二面角E-BF-G的平面角.
在Rt△GHK中,GH=$\frac{3}{2}$,KH=$\frac{3\sqrt{2}}{4}$,
∴tan∠GKH=$\frac{GH}{KH}=\frac{\frac{3}{2}}{\frac{3\sqrt{2}}{4}}=\sqrt{2}$.
点评 本题主要考查直线与平面之间的平行、垂直等位置关系,二面角的概念、求法等知识,以及空间想象能力和逻辑推理能力,是中档题.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:解答题
 如图,矩形ABDE所在平面与正三角形ABC所在平面互相垂直,AE=3,AB=2$\sqrt{3}$,点O是边AB的中点.
如图,矩形ABDE所在平面与正三角形ABC所在平面互相垂直,AE=3,AB=2$\sqrt{3}$,点O是边AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4$\sqrt{3}$ | B. | $\frac{24\sqrt{13}}{13}$ | C. | $\frac{12\sqrt{13}}{13}$ | D. | 8$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,-$\frac{1}{3}$] | B. | [$\frac{1}{5}$,$\frac{1}{3}$) | C. | (-$\frac{1}{3}$,-$\frac{1}{2}$]∪[$\frac{1}{5}$,$\frac{1}{4}$) | D. | [$\frac{1}{4}$,$\frac{1}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
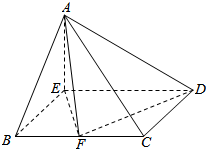 如图所示,在四棱锥A-BCDE中,AE⊥面EBCD且四边形EBCD是菱形,∠BED=120°,AE=BE=2,F是BC上的动点.
如图所示,在四棱锥A-BCDE中,AE⊥面EBCD且四边形EBCD是菱形,∠BED=120°,AE=BE=2,F是BC上的动点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com