
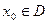 ,使
,使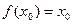 成立,则称以
成立,则称以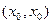 为坐标的点为函数
为坐标的点为函数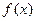 图象上的不动点。
图象上的不动点。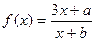 的图象上有两个关于原点对称的不动点,求
的图象上有两个关于原点对称的不动点,求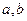 应满足的条件;
应满足的条件;
 , …………………………………………2分
, …………………………………………2分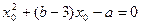 ……………………………………4分
……………………………………4分 即
即 ………6分
………6分 ,
, ,……………………………………………………8分
,……………………………………………………8分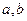 应满足
应满足 且
且 ……………………………………………………10分
……………………………………………………10分 为奇函数,
为奇函数, ,取
,取 ,得
,得 ,
,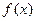 除0以外还有不动点
除0以外还有不动点 ,
,
 ,故
,故 也为函数的不动点。…………………14分
也为函数的不动点。…………………14分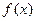 图象上存在有限个不动点,则不动点有奇数个。
图象上存在有限个不动点,则不动点有奇数个。 。…………………………………………………16分
。…………………………………………………16分

 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源:不详 题型:解答题
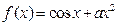 ,当
,当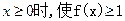 恒成立的a的最小值为k,存在n个
恒成立的a的最小值为k,存在n个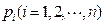 ,且
,且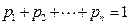 ,任取n个自变量的值
,任取n个自变量的值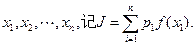
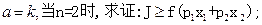
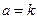 ,且存在n个自变量的值
,且存在n个自变量的值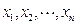 ,使
,使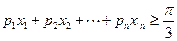 ,求证:
,求证: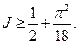
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com