
已知函数f(x)=x2+4ax+2a+6.
(1)若函数f(x)的值域为[0,+∞),求a的值;
(2)若函数f(x)的函数值均为非负数,求g(a)=2-a|a+3|的值域.
(1) 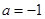 或
或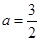 .(2)g (a)的值域为
.(2)g (a)的值域为 .
.
【解析】
试题分析:(1)函数f(x)=x2+4ax+2a+6的值域为[0,+∞),意即这个二次函数的最小值为0,∴Δ=0,
由此便可得a的值.
(2)函数f(x)=x2+4ax+2a+6的值均为非负数,说明这个二次函数的图象的顶点在x轴上或x轴的上方,∴Δ≤0, 由此可求出a的取值范围,从而求出g(a)=2-a|a+3|的值域.
试题解析:(1)∵函数的值域为[0,+∞),
∴Δ=16a2-4(2a+6)=0, ∴2a2-a-3=0, ∴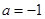 或
或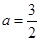 ..
..
(2)∵对一切x∈R函数值均为非负,∴Δ=8 (2a2-a -3)≤0, ∴-1≤a≤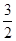 ,∴a+3>0,
,∴a+3>0,
∴g(a)=2-a|a+3|=-a2-3a+2=-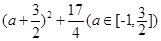 .
.
∵二次函数g (a)在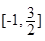 上单调递减,
上单调递减,
∴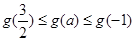 ,即-
,即-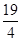 ≤g(a)≤4,∴g (a)的值域为
≤g(a)≤4,∴g (a)的值域为 .
.
考点:二次函数.


科目:高中数学 来源: 题型:
已知函数f(x)=x|m-x|(x∈R),且f(4)=0.
(1)求实数m的值;
(2)作出函数f(x)的图像;
(3)根据图像指出f(x)的单调递减区间;
(4)根据图像写出不等式f(x)>0的解集;
(5)求当x∈[1,5)时函数的值域.
查看答案和解析>>
科目:高中数学 来源:新课标高三数学对数与对数函数、反比例函数与幂函数专项训练(河北) 题型:解答题
已知函数f(x)=loga(x+1),g(x)=2loga(2x+t)(t∈R),其中x∈[0,15],a>0,且a≠1.
(1)若1是关于x的方程f(x)-g(x)=0的一个解,求t的值;
(2)当0<a<1时,不等式f(x)≥g(x)恒成立,求t的取值范围;
查看答案和解析>>
科目:高中数学 来源:2014届江西省高二下学期第二次月考文科数学试卷(解析版) 题型:解答题
已知函数f(x)=|x+1|,g(x)=2|x|+a.
(1)当a=0时,解不等式f(x)≥g(x);
(2)若任意x∈R,f(x) g(x)恒成立,求实数a的取值范围.
g(x)恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013届新课标高三配套第四次月考文科数学试卷(解析版) 题型:解答题
已知函数f(x)= x3+
x3+ x2-ax-a,x∈R,其中a>0.
x2-ax-a,x∈R,其中a>0.
(1)求函数f(x)的单调区间;
(2)若函数f(x)在区间(-2,0)内恰有两个零点,求a的取值范围;
(3)当a=1时,设函数f(x)在区间[t,t+3]上的最大值为M(t),最小值为m(t),记g(t)=M(t)-m(t),求函数g(t)在区间[-3,-1]上的最小值.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖南省、岳阳县一中高三11月联考理科数学 题型:解答题
(本小题满分13分)(第一问8分,第二问5分)
已知函数f(x)=2lnx,g(x)= ax2+3x.
ax2+3x.
(1)设直线x=1与曲线y=f(x)和y=g(x)分别相交于点P、Q,且曲线y=f(x)和y=g(x)在点P、Q处的切线平行,若方程 f(x2+1)+g(x)=3x+k有四个不同的实根,求实数k的取值范围;
f(x2+1)+g(x)=3x+k有四个不同的实根,求实数k的取值范围;
(2)设函数F(x)满足F(x)+x[f′(x)-g′(x)]=-3x2-(a+6)x+1.其中f′(x),g′(x)分别是函数f(x)与g(x)的导函数;试问是否存在实数a,使得当x∈(0,1]时,F(x)取得最大值,若存在,求出a的取值范围;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com