练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

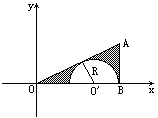
    如图，A为直线y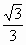＝x上一点，AB⊥x轴于B，半圆的圆心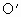在x轴的正半轴上，且半圆与AB，AO相切，已知△ABO绕x轴旋转一周形成的几何体的体积为9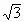π，求阴影部分旋转成的几何体的体积和表面积．

    答案：
    解析：

    分析:阴影部分绕x轴旋转一周所得几何体是圆锥挖去一个内切球的剩余部分，其体积V＝，表面积S＝，设A点坐标为(x，y)，则于是∠AOB＝，从而＝2R，3R＝r＝3，R＝，易算得V＝5π，S＝39π．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：黄冈重点作业·高二数学（下） 题型：044

    如图所示，A为直线y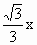＝上一点，AB⊥x轴于B，半圆的圆心在x轴的正半轴上，且半圆与AB、AO相切，已知△ABO绕x轴旋转一周形成的几何体的体积为，求阴影部分旋转成的几何体的体积和表面积．

    查看答案和解析>>

    科目：高中数学 来源：中学教材标准学案　数学　高二上册 题型：044

    已知双曲线S的两条渐近线过坐标原点，且与以点A(，0)为圆心，1为半径的圆相切，双曲线S的一个顶点与点A关于直线y＝x对称．设直线l过点A，斜率为k．

    (1)求双曲线S的方程；

    (2)当k＝1时，在双曲线S的上支上求点B，使其与直线l的距离为；

    (3)当0≤k＜1时，若双曲线S的上支上有且只有一个点B到直线l的距离为，求斜率k的值及相应的点B的坐标．如图．

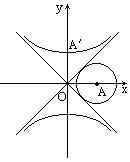
    查看答案和解析>>

    科目：高中数学 来源：高考零距离　二轮冲刺优化讲练　数学 题型：044

    如图所示，已知双曲线S的两条渐近线过坐标原点，且与以点A(，0)为圆心、1为半径的圆相切，双曲线S的一个顶点与点A关于直线y＝x对称．设直线l过点A，斜率为k．

    (1)

    求双曲线S的方程

    (2)

    当k＝1时，在双曲线S的上支上求点B，使其与直线l的距离为

    (3)

    当0≤k＜1时，若双曲线S的上支上有且只有一个点B到直线l的距离为，求斜率k的值及相应的点B的坐标．

    查看答案和解析>>

    科目：高中数学 来源：“伴你学”新课程　数学·必修3、4(人教B版) 人教B版 题型：044

    如图所示为函数y＝f(x)＝Asin(ωx＋)(A＞0，ω＞0，||＜)的一个周期的图象．

    (1)写出y＝f(x)的解析式；

    (2)求y＝g(x)的解析式，使f(x)与g(x)的图象关于直线x＝2对称．

    查看答案和解析>>

    同步练习册答案