
分析 (1)由数列的前n项和求得首项,再由an=Sn-Sn-1(n≥2)求出数列通项公式;
(2)把数列{an}的通项公式代入bn=$\frac{1}{\sqrt{{a}_{n}}+\sqrt{{a}_{n+1}}}$,然后利用裂项相消法求得数列{bn}的前n项和Tn.
解答 解:(1)由Sn=3n2-n,得a1=S1=2;
当n≥2时,${a}_{n}={S}_{n}-{S}_{n-1}=(3{n}^{2}-n)-[3(n-1)^{2}-(n-1)]$
=6n-4.
a1=2适合上式,
∴an=6n-4;
(2)由bn=$\frac{1}{\sqrt{{a}_{n}}+\sqrt{{a}_{n+1}}}$=$\frac{\sqrt{{a}_{n+1}}-\sqrt{{a}_{n}}}{{a}_{n+1}-{a}_{n}}=\frac{1}{6}(\sqrt{{a}_{n+1}}-\sqrt{{a}_{n}})$,
∴Tn=b1+b2+…+bn=$\frac{1}{6}(\sqrt{{a}_{2}}-\sqrt{{a}_{1}}+\sqrt{{a}_{3}}-\sqrt{{a}_{2}}+…+\sqrt{{a}_{n+1}}-\sqrt{{a}_{n}})$
=$\frac{1}{6}(\sqrt{{a}_{n+1}}-\sqrt{{a}_{1}})=\frac{1}{6}(\sqrt{6n+2}-\sqrt{2})$.
点评 本题考查数列递推式,训练了利用裂项相消法求数列的通项公式,是中档题.


 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,+∞) | B. | (-1,3) | C. | (3,+∞) | D. | [3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
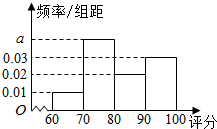 为检测某种零件的生产质量,检验人员需抽取同批次的零件样本进行检测指标评分.若检测后评分结果大于60分的零件为合格零件,评分结果不超过40分的零件将直接被淘汰,评分结果在(40,60]内的零件可能被修复也可能被淘汰.现检验员小张检测出200个合格零件,根据指标评分绘制的频率分布直方图如图所示.
为检测某种零件的生产质量,检验人员需抽取同批次的零件样本进行检测指标评分.若检测后评分结果大于60分的零件为合格零件,评分结果不超过40分的零件将直接被淘汰,评分结果在(40,60]内的零件可能被修复也可能被淘汰.现检验员小张检测出200个合格零件,根据指标评分绘制的频率分布直方图如图所示.| 零件评分结果所在区间 | (40,50] | (50,60] |
| 每个零件个数被修复的概率 | $\frac{1}{3}$ | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$$\overrightarrow{DB}$ | B. | 3$\overrightarrow{MG}$ | C. | 3$\overrightarrow{GM}$ | D. | 2$\overrightarrow{MG}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{16π}{9}$ | B. | $\frac{100π}{9}$ | C. | 25π | D. | 36π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com