
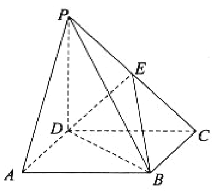
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 是棱
是棱![]() 上的一点.
上的一点.
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() 平面
平面![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,三棱锥![]() 的体积是18,求
的体积是18,求![]() 点到平面
点到平面![]() 的距离.
的距离.
【答案】(1)见解析 ;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)推导出BC⊥PD,BD⊥BC,由此能证明BC⊥平面PBD.(2)连结AC,交BD于O,连结OE,由PA∥平面BDE,得OE∥PA,由此能求出![]() .(3)B到平面PCD的距离d=
.(3)B到平面PCD的距离d=
3![]() ,设PD=a,则
,设PD=a,则![]() =
=![]() ,由三棱锥P﹣BDE的体积是18,求出PD=a=6,设点D到平面PAB的距离为h,由VP﹣ABD=VD﹣PAB,能求出D点到平面PAB的距离.
,由三棱锥P﹣BDE的体积是18,求出PD=a=6,设点D到平面PAB的距离为h,由VP﹣ABD=VD﹣PAB,能求出D点到平面PAB的距离.
(1)∵在四棱锥P﹣ABCD中,底面ABCD是平行四边形,PD⊥平面ABCD,
∴BC⊥PD,∵AD=BD=6,AB=6![]() ,BC=AD,∴BD2+BC2=CD2,∴BD⊥BC,
,BC=AD,∴BD2+BC2=CD2,∴BD⊥BC,
∵PD∩BD=D,∴BC⊥平面PBD.
(2)连结AC交BD于O,连结OE,则O是AC的中点,
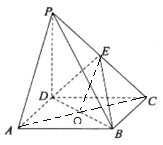
∵PA∥平面BDE,∴OE∥PA,∴E是PC的中点,∴![]() =
=![]() .
.
(3)B到平面PCD的距离d=![]() =3
=3![]() ,设PD=a,则
,设PD=a,则![]() =
=![]()
![]() =
=![]() ,∵三棱锥P﹣BDE的体积是18,∴VP﹣BDE=VB﹣PDE=
,∵三棱锥P﹣BDE的体积是18,∴VP﹣BDE=VB﹣PDE=![]() =
=![]() =18,解得PD=a=6,设点D到平面PAB的距离为h,
=18,解得PD=a=6,设点D到平面PAB的距离为h,
∵PD⊥平面ABCD,AD=BD=6,AB=6![]() ,
,
∴PA=PB=![]() =6
=6![]() ,
,
∴![]() =18
=18![]() ,
,
![]() =
=![]() =18,
=18,
∵VP﹣ABD=VD﹣PAB,∴![]() ,
,
∴h=![]() =
=![]() =2
=2![]() .∴D点到平面PAB的距离为2
.∴D点到平面PAB的距离为2![]() .
.


科目:高中数学 来源: 题型:
【题目】已知动点![]() 到定点
到定点![]() 的距离比
的距离比![]() 到定直线
到定直线![]() 的距离小1.
的距离小1.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)过点![]() 任意作互相垂直的两条直线
任意作互相垂直的两条直线![]() ,分别交曲线
,分别交曲线![]() 于点
于点![]() 和
和![]() .设线段
.设线段![]() ,
, ![]() 的中点分别为
的中点分别为![]() ,求证:直线
,求证:直线![]() 恒过一个定点;
恒过一个定点;
(Ⅲ)在(Ⅱ)的条件下,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】目前某地区有100万人,经过x年后为y万人,如果年平均增长率是1.2%,请回答下列问题:
(1)试推算出y关于x的函数关系式;
(2)计算10年后该地区的人口总数(精确到0.1万人);
(3)计算大约多少年后该地区的人口总数会达到120万(精确到1年).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0,b>0,函数f(x)=|x+a|+|2x-b|的最小值为1.
(1)证明:2a+b=2;
(2)若a+2b≥tab恒成立,求实数t的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】判断下列函数的奇偶性:
(1)f(x)=x+1;
(2)f(x)=x3+3x,x∈[-4,4);
(3)f(x)=|x-2|-|x+2|;
(4)f(x)=
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知袋中装有大小相同的2个白球、2个红球和1个黄球.一项游戏规定:每个白球、红球和黄球的分值分别是0分、1分和2分,每一局从袋中一次性取出三个球,将3个球对应的分值相加后称为该局的得分,计算完得分后将球放回袋中.当出现第![]() 局得
局得![]() 分(
分(![]() )的情况就算游戏过关,同时游戏结束,若四局过后仍未过关,游戏也结束.
)的情况就算游戏过关,同时游戏结束,若四局过后仍未过关,游戏也结束.
(1)求在一局游戏中得3分的概率;
(2)求游戏结束时局数![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面是追踪调查200个某种电子元件寿命(单位:![]() )频率分布直方图,如图:
)频率分布直方图,如图:
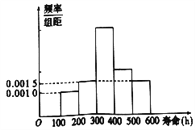
其中300-400、400-500两组数据丢失,下面四个说法中有且只有一个与原数据相符,这个说法是( )
①寿命在300-400的频数是90;
②寿命在400-500的矩形的面积是0.2;
③用频率分布直方图估计电子元件的平均寿命为:
![]()
④寿命超过![]() 的频率为0.3
的频率为0.3
A. ① B. ② C. ③ D. ④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C:x2-y2=1及直线l:y=kx-1.
(1)若l与C有两个不同的交点,求实数k的取值范围;
(2)若l与C交于A,B两点,O为坐标原点,且△AOB的面积为![]() ,求实数k的值.
,求实数k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com