
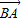 -m
-m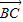 |=|
|=|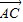 |,则△ABC形状为 .
|,则△ABC形状为 . 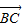 |=(2-2m)|
|=(2-2m)|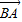 |cos∠B,
|cos∠B,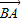 -m
-m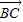 |=|
|=|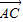 |,∴|
|,∴|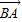 -m
-m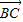 |=|
|=|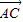 |=|
|=|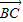 -
-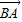 |,
|,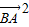 -2m
-2m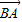 •
•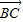 +m2
+m2 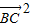 =
=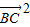 -2
-2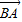
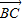 +
+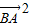 ,
,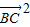 =(2-2m)
=(2-2m)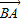
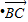 ,∴(1-m2)|
,∴(1-m2)|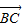 |•|
|•|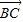 |=(2-2m)|
|=(2-2m)|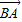 |
|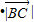 cos∠B,|
cos∠B,|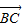 |=(2-2m)|
|=(2-2m)|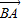 |cos∠B,令 m=-1 得 0=4|
|cos∠B,令 m=-1 得 0=4|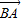 |cos∠B,
|cos∠B,

科目:高中数学 来源:山东省济宁市金乡二中2011-2012学年高二下学期期中考试数学理试题 题型:022
给出下列命题:
①某校开设A类选修课3门,B类选修课4门,一位同学从中共选3门,若要求两类课程中各至少选一门,则不同的选法共有60种;
②对于任意实数x,有f(-x)=-f(x),g(-x)=g(x),且x>0时,![]() (x)>0,
(x)>0,![]() >0,则x<0时,
>0,则x<0时,![]() (x)>
(x)>![]() (x);
(x);
③已知点M在平面ABC内,并且对空间任一点O,![]() =x
=x![]() +
+![]()
![]() +
+![]()
![]() ,则的值为1;
,则的值为1;
④在正三棱柱ABC-A1B1C1中,若AB=2,AA1=1,则点A到平面A1BC的距离为![]() ,其中正确命题的序号是________.
,其中正确命题的序号是________.
查看答案和解析>>
科目:高中数学 来源:四川省南山中学2011-2012学年高二下学期期中考试数学理科试题 题型:022
给出下列命题:
①某校开设A类选修课3门,B类选修课4门,一位同学从中共选3门,若要求两类课程中各至少选一门,则不同的选法共有60种;
②对于任意实数x,有f(-x)=-f(x),g(-x),且x>0时,![]() (x)>0,
(x)>0,![]() (x)>0,则x<0时,
(x)>0,则x<0时,![]() (x)>
(x)>![]() (x);
(x);
③已知点M在平面ABC内,并且对空间任一点O,![]() =x
=x![]() +
+![]()
![]() +
+![]()
![]() ,则x的值为1;
,则x的值为1;
④在正三棱柱ABC-A1B1C1中,若AB=2,AA1=1,则点A到平面A1BC的距离为![]() ,其中正确命题的序号是________
,其中正确命题的序号是________
查看答案和解析>>
科目:高中数学 来源:0114 期中题 题型:解答题
 ,a=3,△ABC的面积为6,
,a=3,△ABC的面积为6, 查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分13分)在△ABC中,![]() 分别为角
分别为角![]() 的对边,
的对边,![]() , △
, △![]() 的面积为6,
的面积为6,
(1)求角![]() 的正弦值;
的正弦值;
⑵求边![]() ;
;
⑶(理科生做)若![]() 为△
为△![]() 内任一点,点
内任一点,点![]() 到三边距离之和为
到三边距离之和为![]() ,求
,求![]() 的取值范围
的取值范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com