
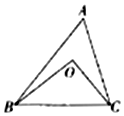
分析 利用余弦定理、直角三角形的性质、三角函数求值即可得出.
解答 解:cosA=$\frac{A{B}^{2}+A{C}^{2}-B{C}^{2}}{2AB•AC}$,连接AO并且延长与BC相交于点D.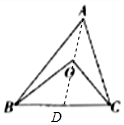
设AD=m,∠ADB=α.
则AB2=${m}^{2}+\frac{B{C}^{2}}{4}$-2×$\frac{BC}{2}$×mcosα,
AC2=m2+$\frac{B{C}^{2}}{4}$-2m×$\frac{BC}{2}$×cos(π-α),
相加可得:AB2+AC2=2m2+$\frac{1}{2}B{C}^{2}$.
m2=(3OD)2=$9×(\frac{1}{2}BC)^{2}$=$\frac{9}{4}B{C}^{2}$.
∴AB2+AC2=5BC2.
又4BC2=AB•AC,
∴cosA=$\frac{1}{2}$,A∈(0,π)
∴A=$\frac{π}{3}$,
故答案为:$\frac{π}{3}$.
点评 本题考查了余弦定理、中线长定理、三角函数求值、直角三角形的性质,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f'(x)=a | B. | f'(x)=b | C. | f'(x0)=a | D. | f'(x0)=b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 1 | 2 | 3 | 4 | 5 |
| f(x) | 4 | 1 | 3 | 5 | 2 |
| A. | 1 | B. | 2 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5:1 | B. | 2:1 | C. | 4:1 | D. | $\sqrt{3}$:1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
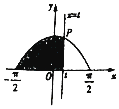 在函数y=cosx,$x∈[{-\frac{π}{2},\frac{π}{2}}]$的图象上有一点P(t,cost),若该函数的图象与x轴、直线$x=-\frac{π}{2},x=t$,围成图形(如图阴影部分)的面积为S,则函数S=g(t)的图象大致是( )
在函数y=cosx,$x∈[{-\frac{π}{2},\frac{π}{2}}]$的图象上有一点P(t,cost),若该函数的图象与x轴、直线$x=-\frac{π}{2},x=t$,围成图形(如图阴影部分)的面积为S,则函数S=g(t)的图象大致是( )| A. | 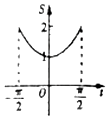 | B. | 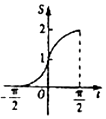 | C. | 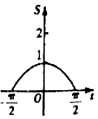 | D. | 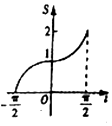 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com