
| A. | 333 | B. | 336 | C. | 1678 | D. | 2015 |
分析 由已知得到函数的周期为6,找到与2015函数值相等的(-3,3)的自变量,按照周期求值.
解答 解:由已知函数周期为6,并且2015=6×335+5,
并且f(1)=1,
f(2)=2,
f(3)=f(-3+6)=f(-3)=-(-3+2)2=-1,
f(4)=f(-2+6)=f(-2)=0,
f(5)=f(-1+6)=f(-1)=-1,
f(6)=f(0)=0,
所以f(1)+f(2)+…+f(6)=1,
所以f(1)+f(2)+…+f(2015)=1×335+f(1)+f(2)+f(3)+f(4)+f(5)=335+1=336;
故选B.
点评 本题考查了函数的周期性的运用;关键是由已知明确所求是几个周期的函数值另外加上前几个自变量的函数值.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,1) | B. | (1,2) | C. | (-1,-2) | D. | (2,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8733 | B. | 8710 | C. | 8726 | D. | 8717 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
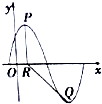 已知函数f(x)=Asin($\frac{π}{3}x$+φ),(A>0,0<φ<$\frac{π}{2}$),y=f(x)的部分图象如图所示,P,Q分别为该图象上相邻的最高点和最低点,点P在x轴上的射影为R(1,0),cos∠PRQ=-$\frac{4}{5}$.
已知函数f(x)=Asin($\frac{π}{3}x$+φ),(A>0,0<φ<$\frac{π}{2}$),y=f(x)的部分图象如图所示,P,Q分别为该图象上相邻的最高点和最低点,点P在x轴上的射影为R(1,0),cos∠PRQ=-$\frac{4}{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com