
【题目】函数![]() 的图象与x轴交于点A,B(点A在点B的左侧),函数
的图象与x轴交于点A,B(点A在点B的左侧),函数![]() 的图象与x轴交于点C,D(点C在点D的左侧),其中
的图象与x轴交于点C,D(点C在点D的左侧),其中![]() ,
,![]() .
.
(1)求证:函数![]() 与
与![]() 的图象交点落在一条定直线上;
的图象交点落在一条定直线上;
(2)若![]() ,求a,b和k应满足的关系式:
,求a,b和k应满足的关系式:
(3)是否存在函数![]() 和
和![]() ,使得B,C为线段AD的三等分点?若存在,求
,使得B,C为线段AD的三等分点?若存在,求![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
【答案】(1)见解析;(2)![]() ;(3)存在,
;(3)存在,![]() 或
或![]()
【解析】
(1)令![]() ,解方程即可求得.
,解方程即可求得.
(2)若![]() ,可得
,可得![]() ,ABCD为抛物线与x轴的交点,求出
,ABCD为抛物线与x轴的交点,求出![]() 的值,代入上式即可求解.
的值,代入上式即可求解.
(3)分类讨论,由BC为线段AD的三等分点,当点B在点C左侧时,![]() ,则有
,则有![]() ,将
,将![]() 代入即可;当点C在点B左侧时,
代入即可;当点C在点B左侧时,![]() ,则有
,则有![]() ,将
,将![]() 代入即可求解.
代入即可求解.
(1)当![]() 时,
时,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴函数![]() 与
与![]() 的图象交点落在一条定直线上;
的图象交点落在一条定直线上;
(2)若![]() ,则
,则![]() ,ABCD为抛物线与x轴的交点,可得
,ABCD为抛物线与x轴的交点,可得
![]() ,
,![]() ,
,
![]()
![]() ,
,
代入![]() 得
得
![]() ,
,
所以![]() ;
;
(3)因为BC为线段AD的三等分点,
当点B在点C左侧时,![]() ,则有
,则有![]() ,
,
∴![]() ,
,
∴![]() ,
,
整理得:![]() ,
,
∴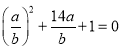 ,
,
解得![]() 或
或![]() ;
;
当点C在点B左侧时,![]() ,则有
,则有![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
整理得:![]() ,
,
∵![]() ,
,
∴![]() ,
,
即![]() ,
,
![]() ,
,
∴ ,
,
![]() ,方程无解,
,方程无解,
综上,![]() 的值为
的值为![]() 或
或![]() .
.


科目:高中数学 来源: 题型:
【题目】“勾股定理”在西方被称为“毕达哥拉斯定理”,三国时期吴国的数学家赵爽创制了一幅“勾股圆方图”,用数形结合的方法给出了勾股定理的详细证明.如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个大正方形.现随机地向大正方形内部区域投掷飞镖,若飞镖落在小正方形区域的概率是![]() ,则直角三角形的两条直角边长的比是(长边:短边)( )
,则直角三角形的两条直角边长的比是(长边:短边)( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】万众瞩目的2018年俄罗斯世界杯决赛于北京时间2018年7月15日23时在俄罗斯莫斯科的卢日尼基体育场进行.为确保总决赛的顺利进行,组委会决定在比赛地点卢日尼基球场外临时围建一个矩形观众候场区,总面积为![]() (如图所示).要求矩形场地的一面利用体育场的外墙,其余三面用铁栏杆围,并且要在体育馆外墙对面留一个长度为
(如图所示).要求矩形场地的一面利用体育场的外墙,其余三面用铁栏杆围,并且要在体育馆外墙对面留一个长度为![]() 的入口.现已知铁栏杆的租用费用为100元/
的入口.现已知铁栏杆的租用费用为100元/![]() .设该矩形区域的长为
.设该矩形区域的长为![]() (单位:
(单位:![]() ),租用铁栏杆的总费用为
),租用铁栏杆的总费用为![]() (单位:元).
(单位:元).

(1)将![]() 表示为
表示为![]() 的函数;
的函数;
(2)试确定![]() ,使得租用此区域所用铁栏杆所需费用最小,并求出最小费用.
,使得租用此区域所用铁栏杆所需费用最小,并求出最小费用.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为保障城市蔬菜供应,某蔬菜种植基地每年投入20万元搭建甲、乙两个无公害蔬菜大棚,每个大棚至少要投入2万元,其中甲大棚种西红柿,乙大棚种黄瓜.根据以往的经验,发现种西红柿的年收入![]() 、种黄瓜的年收入
、种黄瓜的年收入![]() 与大棚投入
与大棚投入![]() 分别满足
分别满足![]() ,
,![]() .设甲大棚的投入为
.设甲大棚的投入为![]() ,每年两个大棚的总收入为
,每年两个大棚的总收入为![]() .(投入与收入的单位均为万元)
.(投入与收入的单位均为万元)
(Ⅰ)求![]() 的值.
的值.
(Ⅱ)试问:如何安排甲、乙两个大棚的投入,才能使年总收人![]() 最大?并求最大年总收入.
最大?并求最大年总收入.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知在平面直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以原点
为参数).以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴,取相同的单位长度建立极坐标系.
轴的非负半轴为极轴,取相同的单位长度建立极坐标系.
(I)求圆![]() 的普通方程及其极坐标方程;
的普通方程及其极坐标方程;
(II)设直线![]() 的极坐标方程为
的极坐标方程为![]() ,射线
,射线![]() 与圆
与圆![]() 的交点为
的交点为![]() ,与直线
,与直线![]() 的交点为Q,求线段PQ的长.
的交点为Q,求线段PQ的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,
中, ![]() ,动点
,动点![]() 满足:以
满足:以![]() 为直径的圆与
为直径的圆与![]() 轴相切.
轴相切.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,直线
,直线![]() 过点
过点![]() 且与
且与![]() 交于
交于![]() 两点,当
两点,当![]() 与
与![]() 的面积之和取得最小值时,求直线
的面积之和取得最小值时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代数学成就的杰出代表.其中《方田》章给出计算弧田面积的经验公式为:![]() .弧田(如图1阴影部分)由圆弧和其所对弦围成,弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.类比弧田面积公式得到球缺(如图 2)近似体积公式:
.弧田(如图1阴影部分)由圆弧和其所对弦围成,弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.类比弧田面积公式得到球缺(如图 2)近似体积公式:![]() 圆面积
圆面积![]() 矢
矢![]() .球缺是指一个球被平面截下的一部分,厦门嘉庚体育馆近似球缺结构(如图3),若该体育馆占地面积约为18000
.球缺是指一个球被平面截下的一部分,厦门嘉庚体育馆近似球缺结构(如图3),若该体育馆占地面积约为18000![]() ,建筑容积约为340000
,建筑容积约为340000![]() ,估计体育馆建筑高度(单位:
,估计体育馆建筑高度(单位:![]() )所在区间为( )
)所在区间为( )
参考数据: ![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() .
.



A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com