
 ��֪P��ԲC����x+1��2+y2=16��������һ�㣬A��1��0�����߶�PA�Ĵ�ֱƽ������PC�ཻ�ڵ�Q��
��֪P��ԲC����x+1��2+y2=16��������һ�㣬A��1��0�����߶�PA�Ĵ�ֱƽ������PC�ཻ�ڵ�Q������ ��1�������߶��д��ߵ����ʿɵ�|QA|=|QP|����|QC|+|QP|=4���뾶����|QC|+|QA|=4��|AC|=2������Բ�Ķ����жϹ켣��Բ�����a��bֵ��������Բ�ı����̣�
��2����y=kx+m����$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$�������ã���3+4k2��x2+8kmx+4m2-12=0������$\overrightarrow{OM}$•$\overrightarrow{ON}$=x1x2+y1y2=x1x2+��kx1+m����kx2+m��=0���ɵ�7m2=12��k2+1��������֤�����ۣ�
��� �⣺��1����Բ�ķ��̿�֪��Բ��C��-1��0�����뾶����4�����Q������Ϊ��x��y ����
���߶�PA�Ĵ�ֱƽ������PC�ཻ�ڵ�Q��
��|QA|=|QP|��
��|QC|+|QP|=4���뾶����
��|QC|+|QA|=4��|AC|=2��
���Q������Բ�Ķ��壬��2a=4��2c=2��
��a=2��c=1��
��b=$\sqrt{3}$��
���M�Ĺ켣����Ϊ$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$��
��2����y=kx+m����$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$���������3+4k2��x2+8kmx+4m2-12=0
��M��x1��y1����N��x2��y2������x1+x2=-$\frac{8km}{3+4{k}^{2}}$��x1x2=$\frac{4{m}^{2}-12}{3+4{k}^{2}}$��
��$\overrightarrow{OM}$•$\overrightarrow{ON}$=x1x2+y1y2=x1x2+��kx1+m����kx2+m��=0��
�ɵ�7m2=12��k2+1����
���O��ֱ��MN�ľ���Ϊh����h=$\frac{|m|}{\sqrt{{k}^{2}+1}}$��
�ڡ�OMN�У��ɵ������֪|MN|h=|OM||ON|
���ԣ�$\frac{1}{|OM{|}^{2}}$+$\frac{1}{|ON{|}^{2}}$=$\frac{|MN{|}^{2}}{|OM{|}^{2}|ON{|}^{2}}$=$\frac{1}{{h}^{2}}$=$\frac{7}{12}$��
���� ���⿼����Բ�Ķ��塢��Բ�ı����̣�����ֱ������Բ��λ�ù�ϵ������ѧ�������������������������е��⣮


 ֥�鿪���γ�������ϵ�д�
֥�鿪���γ�������ϵ�д� ����ѧ��ţ��Ӣ��ϵ�д�
����ѧ��ţ��Ӣ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
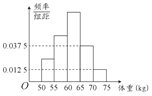 Ϊ���˽���У���걨������Ա��ѧ������������������õ���������������Ƶ�ʷֲ�ֱ��ͼ����ͼ������֪ͼ�д����ҵ�ǰ3��С���Ƶ��֮��Ϊ1��2��3����2С���Ƶ��Ϊ12��������Ա��ѧ�������ǣ�������
Ϊ���˽���У���걨������Ա��ѧ������������������õ���������������Ƶ�ʷֲ�ֱ��ͼ����ͼ������֪ͼ�д����ҵ�ǰ3��С���Ƶ��֮��Ϊ1��2��3����2С���Ƶ��Ϊ12��������Ա��ѧ�������ǣ�������| A�� | 50 | B�� | 47 | C�� | 48 | D�� | 52 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\overrightarrow{b}$=��1��0��0����$\overrightarrow{n}$=��-2��0��0�� | B�� | $\overrightarrow{b}$=��1��3��5����$\overrightarrow{n}$=��1��0��1�� | ||
| C�� | $\overrightarrow{b}$=��0��2��1����$\overrightarrow{n}$=��-1��0��-1�� | D�� | $\overrightarrow{b}$=��1��-1��3����$\overrightarrow{n}$=��0��3��1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com