
【题目】已知函数![]() (其中
(其中![]() ,
, ![]() ).
).
(1)若函数![]() 在
在![]() 上为增函数,求实数
上为增函数,求实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最大值和最小值;
上的最大值和最小值;
(3)当![]() 时,求证:对于任意大于1的正整数
时,求证:对于任意大于1的正整数![]() ,都有
,都有![]() .
.
【答案】(1) ![]() ;(2)最大值是
;(2)最大值是![]() ,最小值是0;(3)证明见解析 .
,最小值是0;(3)证明见解析 .
【解析】试题分析:(1)先求出函数![]() 的导数
的导数![]() ,由题意可知:当
,由题意可知:当![]() 时,
时, ![]() 恒成立,解出
恒成立,解出![]() 的取值范围即可;(2)求导函数,确定函数的单调性,比较端点的函数值,即可求得结论;(3)利用(2)的结论,只要令
的取值范围即可;(2)求导函数,确定函数的单调性,比较端点的函数值,即可求得结论;(3)利用(2)的结论,只要令![]() ,利用放缩法证明即可.
,利用放缩法证明即可.
试题解析:(1) ![]() ,
, ![]()
![]() 函数
函数![]() 在
在![]() 上为增函数,
上为增函数, ![]() 对任意
对任意![]() 恒成立.
恒成立. ![]() 对任意
对任意![]() 恒成立,即
恒成立,即![]() 对任意
对任意![]() 恒成立.
恒成立. ![]() 时,
时, ![]() ,
, ![]() 所求正实数
所求正实数![]() 的取值范围是
的取值范围是![]() .
.
(2)当![]() 时,
时, ![]() ,
, ![]() 当
当![]() 时,
时, ![]() ,故
,故![]() 在
在![]() 上单调递减;
上单调递减; ![]() 当
当![]() 时,
时, ![]() ,故
,故![]() 在
在![]() 上单调递增;
上单调递增;
![]() 在
在![]() 上有唯一的极小值点,也是最小值点,
上有唯一的极小值点,也是最小值点, ![]()
又因为![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]()
所以![]() 在
在![]() 上有的最大值是
上有的最大值是![]()
综上所述, ![]() 在
在![]() 上有的最大值是
上有的最大值是![]() ,最小值是0
,最小值是0
(3)当![]() 时,
时, ![]() ,
, ![]() ,故
,故![]() 在
在![]() 上是增函数.
上是增函数.
当![]() 时,令
时,令![]() ,则当
,则当![]() 时,
时, ![]()
所以 ,即
,即![]()
![]()
所以![]()
对于任意大于1的正整数![]() ,都有
,都有![]() .
.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:
【题目】如图,EP交圆于E,C两点,PD切圆于D,G为CE上一点且PG=PD,连结DG并延长交圆于点A,作弦AB垂直EP,垂足为F.
(Ⅰ)求证:AB为圆的直径;
(Ⅱ)若AC=BD,求证:AB=ED.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义2×2矩阵 ![]() =a1a4﹣a2a3 , 若f(x)=
=a1a4﹣a2a3 , 若f(x)=  ,则f(x)的图象向右平移
,则f(x)的图象向右平移 ![]() 个单位得到函数g(x),则函数g(x)解析式为( )
个单位得到函数g(x),则函数g(x)解析式为( )
A.g(x)=﹣2cos2x
B.g(x)=﹣2sin2x
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知如图:四边形ABCD是矩形,BC⊥平面ABE,且AE=2 ![]() ,EB=BC=2,点F为CE上一点,且BF⊥平面ACE.
,EB=BC=2,点F为CE上一点,且BF⊥平面ACE. 
(1)求证:AE∥平面BFD;
(2)求三棱锥A﹣DBE的体积;
(3)求二面角D﹣BE﹣A的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() 的离心率为
的离心率为![]() ,顶点为
,顶点为![]() ,且
,且![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)![]() 是椭圆
是椭圆![]() 上除顶点外的任意点,直线
上除顶点外的任意点,直线![]() 交
交![]() 轴于点
轴于点![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() .设
.设![]() 的斜率为
的斜率为![]() ,
, ![]() 的斜率为
的斜率为![]() ,试问
,试问![]() 是否为定值?并说明理由.
是否为定值?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准![]() (吨),一位居民的月用水量不超过
(吨),一位居民的月用水量不超过![]() 的部分按平价收费,超过
的部分按平价收费,超过![]() 的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照
的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照![]() ,
, ![]() ,
, ![]() ,
, ![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
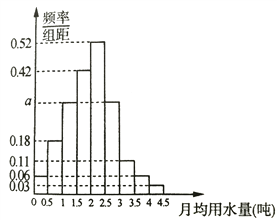
(Ⅰ)求直方图中![]() 的值;
的值;
(Ⅱ)若将频率视为概率,从该城市居民中随机抽取3人,记这3人中月均用水量不低于3吨的人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
(Ⅲ)若该市政府希望使85%的居民每月的用水量不超过标准![]() (吨),估计
(吨),估计![]() 的值(精确到0.01),并说明理由.
的值(精确到0.01),并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某条公共汽车线路收支差额![]() 与乘客量
与乘客量![]() 的函数关系如图所示(收支差额
的函数关系如图所示(收支差额![]() 车票收入
车票收入![]() 支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(Ⅰ)不改变车票价格,减少支出费用;建议(Ⅱ)不改变支出费用,提高车票价格,下面给出的四个图形中,实线和虚线分别表示目前和建议后的函数关系,则
支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(Ⅰ)不改变车票价格,减少支出费用;建议(Ⅱ)不改变支出费用,提高车票价格,下面给出的四个图形中,实线和虚线分别表示目前和建议后的函数关系,则
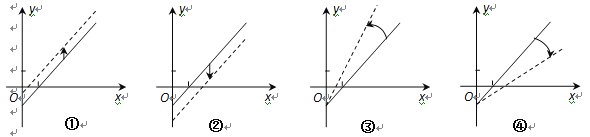
A. ①反映了建议(Ⅱ),③反映了建议(Ⅰ)
B. ①反映了建议(Ⅰ),③反映了建议(Ⅱ)
C. ②反映了建议(Ⅰ),④反映了建议(Ⅱ)
D. ④反映了建议(Ⅰ),②反映了建议(Ⅱ)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l过点P(1,0,﹣1),平行于向量![]() =(2,1,1),平面α过直线l与点M(1,2,3),则平面α的法向量不可能是( )
=(2,1,1),平面α过直线l与点M(1,2,3),则平面α的法向量不可能是( )
A.(1,﹣4,2)
B.(![]() ,-1,
,-1,![]() )
)
C.(-![]() ,1,-
,1,-![]() )
)
D.(0,﹣1,1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com