
| A�� | [0��$\frac{\sqrt{2}}{2}$] | B�� | [$\frac{\sqrt{2}}{2}$��1�� | C�� | [0��$\frac{\sqrt{6}}{3}$] | D�� | [$\frac{\sqrt{2}}{2}$��$\frac{\sqrt{6}}{3}$] |
���� ����ΪF�䣬������Բ���壺|AF|+|AF��|=2a������B��A����ԭ��Գƿ�֪|BF|=|AF��|����֪|AF|+|BF|=2a���ָ���O��Rt��ABF��б���е��֪|AB|=2c����Rt��ABF���á�ABF��c�ֱ��ʾ��|AF|��|BF|����|AF|+|BF|=2a�м��ɱ�ʾ��$\frac{c}{a}$��������e���������ݡ�ABF�ķ�Χȷ��e�ķ�Χ��
��� �⣺��B��A����ԭ��Գƣ���B����Բ�ϣ�
����ΪF�䣬������Բ���壺|AF|+|AF��|=2a��
�֡�|BF|=|AF��|����|AF|+|BF|=2a ����
O��Rt��ABF��б���е㣬��|AB|=2c��
���ABF=������|AF|=2csin����|BF|=2ccos�� ����
�Ѣڴ���ٵã�2csin��+2ccos��=2a��
��$\frac{c}{a}=\frac{1}{sin��+cos��}$����e=$\frac{1}{sin��+cos��}=\frac{1}{\sqrt{2}sin����+\frac{��}{4}��}$��
�ߡ��[$\frac{��}{12}��\frac{��}{4}$]����$\frac{��}{3}��$$��+\frac{��}{4}$��$\frac{��}{2}$��
��$\frac{\sqrt{3}}{2}$��sin����+$\frac{��}{4}$����1��
��$\frac{\sqrt{2}}{2}��e��\frac{\sqrt{6}}{3}$��
��ѡ��D��
���� ������Ҫ��������Բ�����ʣ��ؼ�����Բ�����Ӧ�ã����е��⣮


 Ӧ�����������Ĵ���ѧ������ϵ�д�
Ӧ�����������Ĵ���ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��$\frac{4\sqrt{2}}{9}$ | B�� | $\frac{7}{9}$ | C�� | -$\frac{4\sqrt{2}}{9}$ | D�� | -$\frac{7}{9}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��ֱ�Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
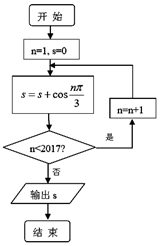
| A�� | -1 | B�� | 0 | C�� | $\frac{1}{2}$ | D�� | $-\frac{3}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com