
 ’直线l:p(cosθ-
’直线l:p(cosθ-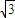 sinθ)=12.
sinθ)=12.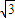 cosθ,
cosθ,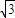 sinθ),求出p点到直线l的距离d=
sinθ),求出p点到直线l的距离d=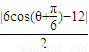 ,可得当 cos(θ+
,可得当 cos(θ+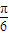 )=1 时,p点到直线l的距离有最小值3.
)=1 时,p点到直线l的距离有最小值3.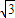 sinθ)=12,即 x-
sinθ)=12,即 x- y-12=0,
y-12=0,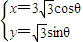 消去参数化为普通方程为
消去参数化为普通方程为 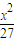 +
+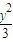 =1.…(5分)
=1.…(5分)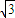 cosθ,
cosθ,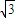 sinθ),
sinθ),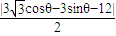 =
= ,
,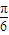 )=1 时,p点到直线l的距离有最小值为3.…(10分)
)=1 时,p点到直线l的距离有最小值为3.…(10分)

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
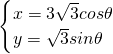 ’直线l:p(cosθ-
’直线l:p(cosθ- sinθ)=12.
sinθ)=12.查看答案和解析>>
科目:高中数学 来源:2012年河南省郑州市高考数学二模试卷(理科)(解析版) 题型:解答题
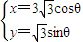 ’直线l:p(cosθ-
’直线l:p(cosθ-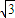 sinθ)=12.
sinθ)=12.查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖北省荆州中学高三第二次质量检查数学试卷(理科)(解析版) 题型:解答题
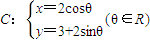 ,一动直线l过A(-1,0)与曲线C相交于P,Q两点,M为P,Q中点,l与直线x+3y+6=0相交于N,则|AM|•|AN|= .
,一动直线l过A(-1,0)与曲线C相交于P,Q两点,M为P,Q中点,l与直线x+3y+6=0相交于N,则|AM|•|AN|= .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com