
【题目】在下列命题中,正确的是( )
A. 垂直于同一个平面的两个平面互相平行 B. 垂直于同一个平面的两条直线互相平行
C. 平行于同一个平面的两条直线互相平行 D. 平行于同一条直线的两个平面互相平行
【答案】B
【解析】对于![]() :垂直于同一个平面的两个平面可能相交,可能平行,故
:垂直于同一个平面的两个平面可能相交,可能平行,故![]() 不正确;对于
不正确;对于![]() :由线面垂直的性质定理可得垂直于同一个平面的两条直线互相平行,故
:由线面垂直的性质定理可得垂直于同一个平面的两条直线互相平行,故![]() 正确;
正确; ![]() :平行于同一个平面的两条直线可能平行,可能相交,可能异面,故
:平行于同一个平面的两条直线可能平行,可能相交,可能异面,故![]() 不正确;
不正确; ![]() :平行于同一条直线的两个平面互相平行,也可能相交,故
:平行于同一条直线的两个平面互相平行,也可能相交,故![]() 不正确,故选B.
不正确,故选B.
【方法点晴】本题主要考查线面平行的判定与性质、面面垂直的性质及线面垂直的判定,属于难题.空间直线、平面平行或垂直等位置关系命题的真假判断,常采用画图(尤其是画长方体)、现实实物判断法(如墙角、桌面等)、排除筛选法等;另外,若原命题不太容易判断真假,可以考虑它的逆否命题,判断它的逆否命题真假,原命题与逆否命题等价.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:
【题目】若函数y=f(x)在R上可导且满足不等式xf′(x)+f(x)>0恒成立,且常数a,b满足a>b,则下列不等式一定成立的是( )
A.af(a)>bf(b)
B.af(b)>bf(a)
C.af(a)<bf(b)
D.af(b)<bf(a)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个函数:①y=3-x;②y=![]() ;③y=x2+2x-10;④y=-
;③y=x2+2x-10;④y=-![]() .其中值域为R的函数个数有( )
.其中值域为R的函数个数有( )
A. 1个 B. 2个
C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用二分法研究函数f(x)=x3+3x﹣1的零点时,第一次经计算f(0)<0,f(0.5)>0,可得其中一个零点x0∈ ,第二次应计算的f(x)的值为f( ).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
, ![]() 为参数),在以
为参数),在以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 是圆心在极轴上,且经过极点的圆.已知曲线
是圆心在极轴上,且经过极点的圆.已知曲线![]() 上的点
上的点 对应的参数
对应的参数![]() ,射线
,射线![]() 与曲线
与曲线![]() 交于点
交于点![]() .
.
(Ⅰ)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若点![]() ,
, ![]() 在曲线
在曲线![]() 上,求
上,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某销售公司为了解员工的月工资水平,从1000位员工中随机抽取100位员工进行调查,得到如下的频率分布直方图:
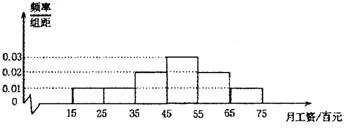
(1)试由此图估计该公司员工的月平均工资;
(2)该公司工资发放是以员工的营销水平为重要依据来确定的,一般认为,工资低于4500。元的员工属于学徒阶段,没有营销经验,若进行营销将会失败;高于4500元的员工是具备营销成熟员工,基进行营销将会成功。现将该样本按照“学徒阶段工资”、“成熟员工工资”分成两层,进行分层抽样,从中抽出5人,在这5人中任选2人进行营销活动。活动中,每位员工若营销成功,将为公司赢得3万元,否则公司将损失1万元。试问在此次比赛中公司收入多少万元的可能性最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)=kax﹣a﹣x(a>0且a≠1)在(﹣∞,+∞)上既是奇函数又是增函数,则函数g(x)=loga(x+k)的图象是( )
A.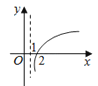
B.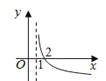
C.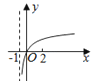
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经国务院批复同意,郑州成功入围国家中心城市,某校学生团针对“郑州的发展环境”对20名学生进行问卷调查打分(满分100分),得到如图1所示茎叶图.
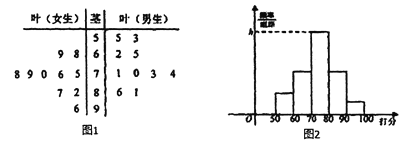
(1)分别计算男生女生打分的平均分,并用数学特征评价男女生打分的数据分布情况;
(2)如图2按照打分区间![]() 绘制的直方图中,求最高矩形的高;
绘制的直方图中,求最高矩形的高;
(3)从打分在70分以下(不含70分)的同学中抽取3人,求有女生被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,分别是椭圆
,分别是椭圆![]() 的左、右焦点.
的左、右焦点.
(1)若点![]() 是第一象限内椭圆上的一点,
是第一象限内椭圆上的一点, ![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)设过定点![]() 的直线
的直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() ,且
,且![]() 为锐角(其中
为锐角(其中![]() 为坐标原点),求直线
为坐标原点),求直线![]() 的斜率
的斜率![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com