
【题目】已知函数![]() .
.
(1)求函数![]() 的极值;
的极值;
(2)若![]() ,试讨论关于
,试讨论关于![]() 的方程
的方程![]() 的解的个数,并说明理由.
的解的个数,并说明理由.
【答案】(1)当![]() 时,
时, ![]() 无极值;当
无极值;当![]() 时,
时, ![]() 有极小值
有极小值![]() ,无极大值。(2)唯一解
,无极大值。(2)唯一解
【解析】试题分析:(1)求出函数的导数,通过讨论m的范围,求出函数的单调区间,从而写出函数的极值;(2)令![]() ,
, ![]() ,问题等价于求
,问题等价于求![]() 函数的零点个数,通过讨论m的范围,判断即可.
函数的零点个数,通过讨论m的范围,判断即可.
试题解析:
(1)依题意得, ![]() ,
, ![]()
当![]() 时,
时, ![]() ,故函数
,故函数![]() 在
在![]() 上单调递增,
上单调递增, ![]() 无极值;
无极值;
当![]() 时,令
时,令![]() ,
, ![]() 或
或![]() (舍)
(舍)
当![]() 时,
时, ![]() ,函数
,函数![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时, ![]() ,函数
,函数![]() 在
在![]() 上单调递增.
上单调递增.
故函数![]() 有极小值
有极小值![]() .
.
综上所述:当![]() 时,
时, ![]() 无极值;
无极值;
当![]() 时,
时, ![]() 有极小值
有极小值![]() ,无极大值.
,无极大值.
(2)令![]() ,
, ![]() ,问题等价于求
,问题等价于求![]() 函数的零点个数.
函数的零点个数.
易得![]()
当![]() 时,
时, ![]() ,函数
,函数![]() 为减函数,因为
为减函数,因为![]() ,
, ![]() ,所以
,所以![]() 有唯一零点;
有唯一零点;
当![]() 时,则当
时,则当![]() 或
或![]() 时,
时, ![]() ,而当
,而当![]() 时,
时, ![]() ,
,
所以,函数![]() 在
在![]() 和
和![]() 上单调递减,在
上单调递减,在![]() 单调递增,
单调递增,
因为![]() ,
, ![]() ,所以函数
,所以函数![]() 有唯一零点.
有唯一零点.
综上,若![]() ,函数
,函数![]() 有唯一零点,即方程方程
有唯一零点,即方程方程![]() 有唯一解.
有唯一解.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 是定义在
是定义在![]() 上的奇函数.
上的奇函数.
(1)当![]() 时,
时, ![]() ,若当
,若当![]() 时,
时, ![]() 恒成立,求
恒成立,求![]() 的最小值;
的最小值;
(2)若![]() 的图像关于
的图像关于![]() 对称,且
对称,且![]() 时,
时, ![]() ,求当
,求当![]() 时,
时, ![]() 的解析式;
的解析式;
(3)当![]() 时,
时, ![]() .若对任意的
.若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1 , F2为椭圆 ![]() 的左、右焦点,F2在以
的左、右焦点,F2在以 ![]() 为圆心,1为半径的圆C2上,且|QF1|+|QF2|=2a.
为圆心,1为半径的圆C2上,且|QF1|+|QF2|=2a.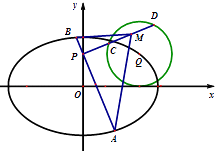
(1)求椭圆C1的方程;
(2)过点P(0,1)的直线l1交椭圆C1于A,B两点,过P与l1垂直的直线l2交圆C2于C,D两点,M为线段CD中点,求△MAB面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
(1)证明PA∥平面EDB;
(2)证明PB⊥平面EFD;
(3)求二面角C﹣PB﹣D的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四组函数中,表示相等函数的一组是( )
A.f(x)=1,g(x)=x0?
B.f(x)=|x|,g(t)= ![]()
C.f(x)= ![]() ,g(x)=x+1?
,g(x)=x+1?
D.f(x)=lg(x+1)+lg(x﹣1),g(x)=lg(x2﹣1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为R,若存在常数T≠0,使得f(x)=Tf(x+T)对任意的x∈R成立,则称函数f(x)是Ω函数. (Ⅰ)判断函数f(x)=x,g(x)=sinπx是否是Ω函数;(只需写出结论)
(Ⅱ)说明:请在(i)、(ii)问中选择一问解答即可,两问都作答的按选择(i)计分
(i)求证:若函数f(x)是Ω函数,且f(x)是偶函数,则f(x)是周期函数;
(ii)求证:若函数f(x)是Ω函数,且f(x)是奇函数,则f(x)是周期函数;
(Ⅲ)求证:当a>1时,函数f(x)=ax一定是Ω函数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com