
【题目】已知点![]() ,点A是直线
,点A是直线![]() 上的动点,过
上的动点,过![]() 作直线
作直线![]() ,
,![]() ,线段
,线段![]() 的垂直平分线与
的垂直平分线与![]() 交于点
交于点![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)若点![]() ,
,![]() 是直线
是直线![]() 上两个不同的点,且
上两个不同的点,且![]() 的内切圆方程为
的内切圆方程为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)根据题意得到:点![]() 到点
到点![]() 的距离等于它到直线
的距离等于它到直线![]() 的距离,所以点
的距离,所以点![]() 的轨迹是以点F为焦点,直线
的轨迹是以点F为焦点,直线![]()
![]() 为准线的抛物线,再利用抛物线的定义即可得到曲线
为准线的抛物线,再利用抛物线的定义即可得到曲线![]() 的方程.
的方程.
(2)首先设![]() ,点
,点![]() ,点
,点![]() ,求出直线
,求出直线![]() 的方程,根据圆心
的方程,根据圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,得到
,得到![]() ,同理得到
,同理得到![]() ,即
,即![]() 是关于
是关于![]() 的方程
的方程![]() 的两根,再根据韦达定理得到
的两根,再根据韦达定理得到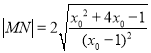 ,再求
,再求![]() 的范围即可.
的范围即可.
(1)因为点![]() ,点
,点![]() 是直线
是直线![]()
![]() 上的动点,
上的动点,
过![]() 作直线
作直线![]() ,
,![]() ,线段
,线段![]() 的垂直平分线与
的垂直平分线与![]() 交于点
交于点![]() ,
,
所以点![]() 到点
到点![]() 的距离等于它到直线
的距离等于它到直线![]() 的距离,
的距离,
所以点![]() 的轨迹是以点F为焦点,直线
的轨迹是以点F为焦点,直线![]()
![]() 为准线的抛物线,
为准线的抛物线,
所以曲线![]() 的方程为
的方程为![]() .
.
(2)设![]() ,点
,点![]() ,点
,点![]() ,
,
直线![]() 的方程为:
的方程为:![]() ,
,
化简得![]() ,
,
因为![]() 的内切圆的方程为
的内切圆的方程为![]() ,
,
所以圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,即
,即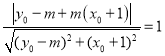 ,
,
整理得:![]() ,
,
由题意得![]() ,所以上式化简得
,所以上式化简得![]() ,
,
同理,有![]() .
.
所以![]() 是关于
是关于![]() 的方程
的方程![]() 的两根,
的两根,
![]() ,
,![]() .
.
所以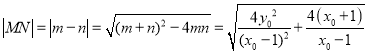 ,
,
因为![]() ,
,![]() ,
,
所以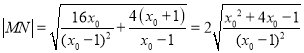 ,
,
直线![]() 的斜率
的斜率![]() ,则
,则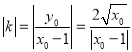 ,
,
所以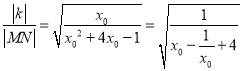 ,
,
因为函数![]() 在
在![]() 单调递增,
单调递增,
所以![]() ,
,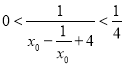 ,
,
所以0![]() .
.
即![]() 的取值范围是
的取值范围是![]() .
.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案科目:高中数学 来源: 题型:
【题目】已知曲线C的参数方程为![]() (
(![]() 为参数),P是曲线C上的点且对应的参数为
为参数),P是曲线C上的点且对应的参数为![]() ,
,![]() .直线l过点P且倾斜角为
.直线l过点P且倾斜角为![]() .
.
(1)求曲线C的普通方程和直线l的参数方程.
(2)已知直线l与x轴,y轴分别交于![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 垂直圆O所在的平面,
垂直圆O所在的平面,![]() 是圆O的一条直径,C为圆周上异于A,B的动点,D为弦
是圆O的一条直径,C为圆周上异于A,B的动点,D为弦![]() 的中点,
的中点,![]() .
.
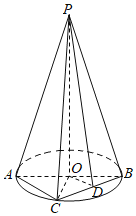
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列{an}的前n项和Sn满足2Sn=an+2﹣2,n∈N*.
(1)若数列{an}为等比数列,求数列{an}的公比q的值.
(2)若a2=a1=1,bn=an+an+1,求数列{bn}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校某班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图(已知本次测试成绩满分100分,且均为不低于50分的整数),请根据图表中的信息解答下列问题.
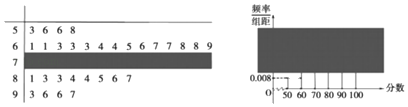
(1)求全班的学生人数及频率分布直方图中分数在[70,80)之间的矩形的高;
(2)为了帮助学生提高数学成绩,决定在班里成立“二帮一”小组,即从成绩[90,100]中选两位同学,共同帮助[50,60)中的某一位同学,已知甲同学的成绩为53分,乙同学的成绩为96分,求甲、乙恰好被安排在同一小组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在《九章算术》中,将四个面都为直角三角形的四面体称之为鳖臑.如图,在鳖臑![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,且
,且![]() ,过点
,过点![]() 分别作
分别作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,连结
,连结![]() ,当
,当![]() 的面积最大值时,
的面积最大值时,![]() ( ).
( ).
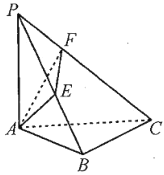
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】半正多面体亦称“阿基米德多面体”,是由边数不全相同的正多边形为面的多面体,体现了数学的对称美.如图,将正方体沿交于一顶点的三条棱的中点截去一个三棱锥,如此共可截去八个三棱锥,得到一个有十四个面的半正多面体,它们的棱长都相等,其中八个为正三角形,六个为正方形,称这样的半正多面体为二十四等边体.若棱长为![]() 的二十四等边体的各个顶点都在同一个球面上,则该球的表面积为( )
的二十四等边体的各个顶点都在同一个球面上,则该球的表面积为( )
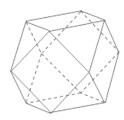
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小军的微信朋友圈参与了“微信运动”,他随机选取了40位微信好友(女20人,男20人),统计其在某一天的走路步数.其中,女性好友的走路步数数据记录如下:
5860 8520 7326 6798 7325 8430 3216 7453 11754 9860
8753 6450 7290 4850 10223 9763 7988 9176 6421 5980
男性好友走路的步数情况可分为五个类别(说明:a~b表示大于等于a,小于等于b)
A(0~2000步)1人, B(2001-5000步)2人, C(5001~8000步)3人,
D(8001-10000步)6人, E(10001步及以上)8人
若某人一天的走路步数超过8000步被系统认定为“健康型”否则被系统认定为“进步型”.
(I)访根据选取的样本数据完成下面的2×2列联表,并根据此判断能否有95%以上的把握认为“认定类型”与“性别”有关?
健康型 | 进步型 | 总计 | |
男 | 20 | ||
女 | 20 | ||
总计 | 40 |
(Ⅱ)如果从小军的40位好友中该天走路步数超过10000的人中随机抽取3人,设抽到女性好友X人,求X的分布列和数学期望![]() .
.
附:![]()
![]() .
.
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com