
【题目】如图程序框图的算法思路源于我国古代数学名著《九章算术》中的某一种算法.执行该程序框图,输入分别为98,63,则输出的结果是( ) 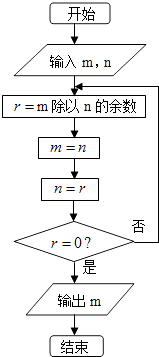
A.14
B.18
C.9
D.7
科目:高中数学 来源: 题型:
【题目】如图,已知三棱锥O﹣ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.

(1)求异面直线BE与AC所成角的余弦值;
(2)求直线BE和平面ABC的所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为常数,函数
为常数,函数![]() .
.
(1)当![]() 时,求关于
时,求关于![]() 的不等式
的不等式![]() 的解集;
的解集;
(2)当![]() 时,若函数
时,若函数![]() 在
在![]() 上存在零点,求实数
上存在零点,求实数![]() 的取值范围;
的取值范围;
(3)当![]() 时,对于给定的
时,对于给定的![]() ,且
,且![]() ,
,![]() ,证明:关于
,证明:关于![]() 的方程
的方程![]() 在区间
在区间![]() 内有一个实根.
内有一个实根.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx,g(x)=(﹣x2+ax﹣3)ex(a为实数).
(1)当a=4时,求函数y=g(x)在x=0处的切线方程;
(2)求f(x)在区间[t,t+2](t>0)上的最小值;
(3)如果关于x的方程g(x)=2exf(x)在区间[ ![]() ,e]上有两个不等实根,求实数a的取值范围.
,e]上有两个不等实根,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将圆x2+y2=1上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线C.
(1)写出C的参数方程;
(2)设直线l:2x+y﹣2=0与C的交点为P1 , P2 , 以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段P1P2的中点且与l垂直的直线的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为正方形,平面
为正方形,平面![]() 底面
底面![]() ,
, ![]() ,点
,点![]() 分别是
分别是![]() 的中点.
的中点.

(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求证: ![]() 平面
平面![]() ;
;
(Ⅲ)在棱![]() 上求作一点
上求作一点![]() ,使得
,使得![]() ,并说明理由.
,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 圆![]() ,过点
,过点![]() 作圆
作圆![]() 的切线,切点分别为
的切线,切点分别为![]() 、
、![]() ,且
,且![]() (
(![]() 为原点).
为原点).
(![]() )求点
)求点![]() 的轨迹方程.
的轨迹方程.
(![]() )求四边形
)求四边形![]() 面积的最小值.
面积的最小值.
(![]() )设
)设![]() ,
, ![]() ,在圆
,在圆![]() 上存在点
上存在点![]() ,使得
,使得![]() ,求
,求![]() 的最大值和最小值(直接写出结果即可).
的最大值和最小值(直接写出结果即可).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com