
【题目】已知函数f(x)=mx-lnx-1(m为常数).
(1)若函数f(x)恰有1个零点,求实数m的取值范围;
(2)若不等式mx-ex≤f(x)+a对正数x恒成立,求实数a的最小整数值.
【答案】(1){m|m≤0或m=1}(2)实数a的最小整数值为-1
【解析】
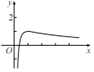
(1)首先写出f(x)的定义域,函数f(x)恰有1个零点方程f(x)=0仅有一个正实数解,由f(x)=0,得![]() ,设g(x)
,设g(x)![]() ,然后求导,找出g(x)的最值,结合图象求出m的范围;
,然后求导,找出g(x)的最值,结合图象求出m的范围;
(2)mx-ex≤f(x)+alnx-ex≤a-1.设h(x)=lnx-ex,求导判断h(x)的单调区间,利用单调性求出a的最值即可.
解:(1)f(x)的定义域为(0,+∞),
函数f(x)恰有1个零点方程f(x)=0仅有一个正实数解,
由f(x)=0,得![]() ,
,
设g(x)![]() ,则
,则![]() ,
,
令g′(x)>0.得0<x<1,
令g′(x)<0,得x>1,
∴g(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
∴g(x)在x=1处取得唯一的极大值,即为最大值,
故g(x)的最大值为g(1)=1.
当x趋近于0时,lnx+1趋近于-∞,
所以g(x)为负数,
当x趋近于+∞时,x的增长速度大于lnx+1的增长速度,
且当x>1时![]() ,
,
故g(x)趋近于0,
由图可知,当m≤0或者m=1时,方程m=g(x)仅有一个实数解,
∴m的取值范围为{m|m≤0或m=1};
(2)∵mx-ex≤f(x)+a,
∴lnx-ex≤a-1,
设h(x)=lnx-ex,
∴![]()
又∵![]() 在(0,+∞)上为减函数,h′(1)=1-e<0,
在(0,+∞)上为减函数,h′(1)=1-e<0,![]() ,
,
∴![]() 存在唯一的零点
存在唯一的零点![]() ,
,
此时h(x)在(0,x0)上单调递增,在(x0,+∞)上单调递减,/p>
且![]() =0,
=0,
∴![]() ,x0=-lnx0,
,x0=-lnx0,
由单调性知![]() =-(x0+
=-(x0+![]() ),
),
又![]() ,故
,故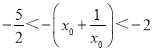 ,
,
∴mx-ex≤f(x)+a对任意正数x恒成立时,a-1≥-2,
∴a≥-1,
∴实数a的最小整数值为-1.


科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() ,(
,( ![]() 为参数),
为参数),![]() 为曲线
为曲线![]() 上的动点,动点
上的动点,动点![]() 满足
满足![]() (
(![]() 且
且![]() ),
),![]() 点的轨迹为曲线
点的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程,并说明
的方程,并说明![]() 是什么曲线;
是什么曲线;
(2)在以坐标原点为极点,以![]() 轴的正半轴为极轴的极坐标系中,
轴的正半轴为极轴的极坐标系中, ![]() 点的极坐标为
点的极坐标为![]() ,射线
,射线![]() 与
与![]() 的异于极点的交点为
的异于极点的交点为![]() ,已知
,已知![]() 面积的最大值为
面积的最大值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,已知直线l过点P(2,2).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ﹣ρcos2θ﹣4cosθ=0.
(1)求C的直角坐标方程;
(2)若l与C交于A,B两点,求 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
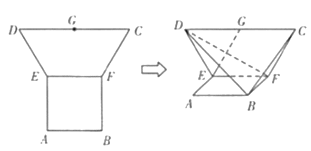
【题目】在平面多边形![]() 中,四边形
中,四边形![]() 是边长为2的正方形,四边形
是边长为2的正方形,四边形![]() 为等腰梯形,
为等腰梯形,![]() 为
为![]() 的中点,
的中点,![]() ,现将梯形
,现将梯形![]() 沿
沿![]() 折叠,使平面
折叠,使平面![]() 平面
平面![]() .
.
(1)求证:![]() 面
面![]() ;
;
(2)求![]() 与平面
与平面![]() 成角的正弦值.
成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com