
分析 画出△ABC绕直线l旋转一周所得到的几何体的直观图,结合圆台和圆锥的侧面积及底面积公式,可得答案.
解答 解:∵直线l过A且与AB垂直,
将△ABC绕直线l旋转一周所得到的几何体如下图所示: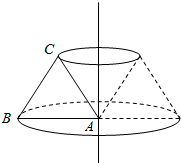
所得几何体的表面积由圆台的下底面积,圆台的侧面积,圆锥的侧面积组成,
由圆台的下底半径为a,可得圆台的下底面积为πa2,
由圆台的上底(圆锥的底面)半径为$\frac{1}{2}$a,圆台的母线长为a,可得圆台的侧面积为${\frac{3}{2}πa}^{2}$,
由圆锥的母线长为a,可得圆锥的侧面积为${\frac{1}{2}πa}^{2}$,
综上几何体的表面积为:3πa2,
故答案为:3πa2
点评 本题考查的知识点是旋转体,熟练掌握圆台和圆锥的侧面积及底面积公式,是解答的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | P>Q | B. | P<Q | C. | P≤Q | D. | 无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,椭圆C1:x2+$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的左、右顶点分别为A,B,点P为双曲线C2:x2-$\frac{{y}^{2}}{{b}^{2}}$=1在第一象限内的图象上一点,直线AP,BP与椭圆C1分别交于C,D两点.C是AP的中点.
如图,椭圆C1:x2+$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的左、右顶点分别为A,B,点P为双曲线C2:x2-$\frac{{y}^{2}}{{b}^{2}}$=1在第一象限内的图象上一点,直线AP,BP与椭圆C1分别交于C,D两点.C是AP的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com