
分析:由f(x)=x
2-2kx+k=(x-k)
2+k-k
2,对称轴x=k,①当k≤0时,函数f(x)在[0,1]上单调递增,当x=0时,函数有最小值f(0);②当0<k<1时,函数f(x)在[0,k)单调递减,在(k,1]单调递增,当x=k时函数有最小值;③当k≥1时,函数f(x)在[0,1]上单调递减,当x=1时,函数有最小值f(1,结合已知可求
解答:∵f(x)=x
2-2kx+k=(x-k)
2+k-k
2,对称轴x=k
①当k≤0时,函数f(x)在[0,1]上单调递增,当x=0时,函数有最小值f(0)=k=

,不符合题意
②当0<k<1时,函数f(x)在[0,k)单调递减,在(k,1]单调递增,当x=k时函数有最小值k-

,解可得k=

,符合题意
③当k≥1时,函数f(x)在[0,1]上单调递减,当x=1时,函数有最小值f(1)=1-k=

,解可得k=

不符合题意
综上可得,k=

故答案为:

点评:本题主要考查了二次函数在闭区间上的最值的求解,解决此类问题的关键是确定函数在所给区间的单调性,而当单调性不确定时,需要分类讨论

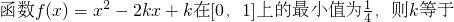 ________.
________.
 ,不符合题意
,不符合题意 ,解可得k=
,解可得k= ,符合题意
,符合题意 ,解可得k=
,解可得k= 不符合题意
不符合题意



 ;
;