
【题目】设抛物线![]() 的焦点为F,已知直线
的焦点为F,已知直线![]() 与抛物线C交于A,B两点(A,B两点分别在
与抛物线C交于A,B两点(A,B两点分别在![]() 轴的上、下方).
轴的上、下方).
(1)求证:![]() ;
;
(2)已知弦长![]() ,试求:过A,B两点,且与直线
,试求:过A,B两点,且与直线![]() 相切的圆D的方程.
相切的圆D的方程.
【答案】(1)见解析;(2)![]() 或
或![]()
【解析】
(1) 由![]() 与
与![]() 得
得![]() ,解得
,解得 ![]() ,又
,又![]() ,从而得到结果;(2) 由弦长
,从而得到结果;(2) 由弦长![]() 及抛物线定义可得m=1.圆心D在线段AB的中垂线上,求出中垂线方程,设出所求圆的圆心坐标为
及抛物线定义可得m=1.圆心D在线段AB的中垂线上,求出中垂线方程,设出所求圆的圆心坐标为![]() ,借助点到线的距离公式可得圆D的方程.
,借助点到线的距离公式可得圆D的方程.
(1)由![]() 与
与![]() 消去x,得
消去x,得![]() ,
,
设![]() ,
,
则![]() 为方程
为方程![]() 的两个不同的根,
的两个不同的根,
所以![]() ,
,
因为A,F,B三点共线,所以![]()
(2)因为AB=8,
所以![]() .
.
所以![]() ,
,
所以m=1.
线段AB的中点坐标为(3m,2m),即(3,2),
所以线段AB的中垂线方程为![]() ,
,
因为所求的圆过A,B点,所以圆心D在直线![]() 上,
上,
设所求圆的圆心坐标为![]() ,
,
不难算得两条平行线![]() 与
与![]()
之间的距离![]() ,
,
即D到直线![]() 的距离
的距离![]() ,
,
由D到直线![]() 的距离得
的距离得![]() .
.
设圆D的半径为R,
则![]() ,
,
因为过点A与点B的圆与直线![]() 相切,所以
相切,所以![]() ,
,
所以![]() ,
,
解得![]() ,或
,或![]() ,
,
所以所求圆的方程为![]() 或
或![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,椭圆![]()
![]() 的左右焦点分别为的
的左右焦点分别为的![]() 、
、![]() ,离心率为
,离心率为![]() ;过抛物线
;过抛物线![]() 焦点
焦点![]() 的直线交抛物线于
的直线交抛物线于![]() 、
、![]() 两点,当
两点,当![]() 时,
时, ![]() 点在
点在![]() 轴上的射影为
轴上的射影为![]() 。连结
。连结![]() 并延长分别交
并延长分别交![]() 于
于![]() 、
、![]() 两点,连接
两点,连接![]() ;
; ![]() 与
与![]() 的面积分别记为
的面积分别记为![]() ,
, ![]() ,设
,设![]() .
.
(Ⅰ)求椭圆![]() 和抛物线
和抛物线![]() 的方程;
的方程;
(Ⅱ)求![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,建立平面直角坐标系![]() ,
,![]() 轴在地平面上,
轴在地平面上,![]() 轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程
轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程![]() 表示的曲线上,其中
表示的曲线上,其中![]() 与发射方向有关.炮的射程是指炮弹落地点的横坐标.
与发射方向有关.炮的射程是指炮弹落地点的横坐标.

(1)求炮的最大射程;
(2)设在第一象限有一飞行物(忽略其大小),其飞行高度为3.2千米,试问它的横坐标![]() 不超过多少时,炮弹可以击中它?请说明理由.
不超过多少时,炮弹可以击中它?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了激励业务员的积极性,对业绩在60万到200万的业务员进行奖励奖励方案遵循以下原则:奖金y(单位:万元)随着业绩值x(单位:万元)的增加而增加,且奖金不低于1.5万元同时奖金不超过业绩值的5%.
(1)若某业务员的业绩为100万核定可得4万元奖金,若该公司用函数![]() (k为常数)作为奖励函数模型,则业绩200万元的业务员可以得到多少奖励?(已知
(k为常数)作为奖励函数模型,则业绩200万元的业务员可以得到多少奖励?(已知![]() ,
,![]() )
)
(2)若采用函数![]() 作为奖励函数模型试确定最小的正整数a的值.
作为奖励函数模型试确定最小的正整数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】7人排成一排,按以下要求分别有多少种排法?
(1)甲、乙两人排在一起;
(2)甲不在左端、乙不在右端;
(3)甲、乙、丙三人中恰好有两人排在一起.(答题要求:先列式,后计算)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知p:x2-(3+a)x+3a<0,其中a<3;q:x2+4x-5>0.
(1)若p是q的必要不充分条件,求实数a的取值范围;
(2)若p是q的充分不必要条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
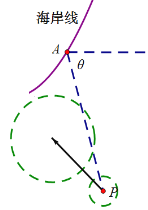
【题目】在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市A(看做一点)的东偏南![]() 角方向
角方向![]() ,300 km的海面P处,并以20km / h的速度向西偏北45°方向移动.台风侵袭的范围为圆形区域,当前半径为60 km,并以10km / h的速度不断增大.
,300 km的海面P处,并以20km / h的速度向西偏北45°方向移动.台风侵袭的范围为圆形区域,当前半径为60 km,并以10km / h的速度不断增大.
(1) 问10小时后,该台风是否开始侵袭城市A,并说明理由;
(2) 城市A受到该台风侵袭的持续时间为多久?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com