
【题目】已知定义域为![]() 的函数
的函数![]() 满足:(1)对任意
满足:(1)对任意![]() ,恒有
,恒有![]() 成立;(2)当
成立;(2)当![]() 时,
时,![]() .给出如下结论:
.给出如下结论:
①对任意![]() ,有
,有![]() ;
;
②函数![]() 的值域为
的值域为![]()
③存在![]() ,使得
,使得![]() ;
;
④“函数![]() 在区间
在区间![]() 上单调递减”的充要条件是“存在
上单调递减”的充要条件是“存在![]() ,使得
,使得![]() ”.
”.
上述结论正确有( )
A.1个B.2个C.3个D.4个
【答案】C
【解析】
依据题中条件注意研究每个选项的正确性,连续利用题中第(1)个条件得到①正确;连续利用题中第(2)个条件得到②正确;利用反证法及2x变化如下:2,4,8,16,32,判断③命题错误;据①②③的正确性可得④是正确的.
①f(2m)=f(22m﹣1)=2f(2m﹣1)=…=2m﹣1f(2),正确;
②取x∈(2m,2m+1],则![]() ∈(1,2];f(
∈(1,2];f(![]() )=2
)=2![]() ,从而
,从而
f(x)=2f(![]() )=…=2mf(
)=…=2mf(![]() )=2m+1﹣x,其中,m=0,1,2,…
)=2m+1﹣x,其中,m=0,1,2,…
从而f(x)∈[0,+∞),正确;
③f(2n+1)=2n+1﹣2n﹣1,假设存在n使f(2n+1)=9,即存在x1,x2,![]() 10,又,2x变化如下:2,4,8,16,32,显然不存在,所以该命题错误;
10,又,2x变化如下:2,4,8,16,32,显然不存在,所以该命题错误;
④根据前面的分析容易知道该选项正确;
综合有正确的序号是①②④.
故选:C.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】随着经济的发展,个人收入的提高,自2019年1月1日起,个人所得税起征点和税率作了调整.调整如下:纳税人的工资、薪金所得,以每月全部收入额减除5000元后的余额为应纳税所得额.依照个人所得税税率表,调整前后的计算方法如下表:
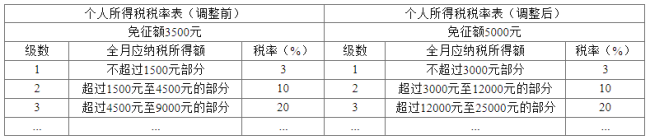
(1)假如小明某月的工资、薪金等税前收入为7500元,请你帮小明算一下调整后小明的实际收入比调整前增加了多少?
(2)某税务部门在小明所在公司利用分层抽样方法抽取某月100个不同层次员工的税前收入,并制成下面的频数分布表:
![]()
先从收入在![]() 及
及![]() 的人群中按分层抽样抽取7人,再从中选3人作为新纳税法知识宣讲员,用随机变量
的人群中按分层抽样抽取7人,再从中选3人作为新纳税法知识宣讲员,用随机变量![]() 表示抽到作为宣讲员的收入在
表示抽到作为宣讲员的收入在![]() 元的人数,求
元的人数,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是定义在R上的两个周期函数,
是定义在R上的两个周期函数,![]() 的周期为4,
的周期为4,![]() 的周期为2,且
的周期为2,且![]() 是奇函数.当
是奇函数.当![]() 时,
时,![]() ,
,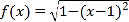 ,其中k>0.若在区间(0,9]上,关于x的方程
,其中k>0.若在区间(0,9]上,关于x的方程![]() 有8个不同的实数根,则k的取值范围是_____.
有8个不同的实数根,则k的取值范围是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有10个不同的产品,其中4个次品,6个正品.现每次取其中一个进行测试,直到4个次品全测完为止,若最后一个次品恰好在第五次测试时被发现,则该情况出现的概率是_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的圆心为
的圆心为![]() ,直线l过点
,直线l过点![]() 且与x轴不重合,l交圆
且与x轴不重合,l交圆![]() 于C,D两点,过
于C,D两点,过![]() 作
作![]() 的平行线,交
的平行线,交![]() 于点E.设点E的轨迹为
于点E.设点E的轨迹为![]() .
.
(1)求![]() 的方程;
的方程;
(2)直线![]() 与
与![]() 相切于点M,
相切于点M,![]() 与两坐标轴的交点为A与B,直线
与两坐标轴的交点为A与B,直线![]() 经过点M且与
经过点M且与![]() 垂直,
垂直,![]() 与
与![]() 的另一个交点为N,当
的另一个交点为N,当![]() 取得最小值时,求
取得最小值时,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的焦距为4,且过点
的焦距为4,且过点![]() .
.
(1)求椭圆![]() 的方程
的方程
(2)设椭圆![]() 的上顶点为
的上顶点为![]() ,右焦点为
,右焦点为![]() ,直线
,直线![]() 与椭圆交于
与椭圆交于![]() 、
、![]() 两点,问是否存在直线
两点,问是否存在直线![]() ,使得
,使得![]() 为
为![]() 的垂心,若存在,求出直线
的垂心,若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4 坐标系与参数方程选讲
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程
的参数方程 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的非负半轴为极轴,建立极坐标系,曲线
轴的非负半轴为极轴,建立极坐标系,曲线![]() 极坐标方程为
极坐标方程为![]() .
.
(1)求直线![]() 的普通方程以及曲线
的普通方程以及曲线![]() 的参数方程;
的参数方程;
(2)当![]() 时,
时,![]() 为曲线
为曲线![]() 上动点,求点
上动点,求点![]() 到直线
到直线![]() 距离的最大值.
距离的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com