
【题目】关于函数![]() ,下列判断正确的是( )
,下列判断正确的是( )
A.![]() 是
是![]() 的极大值点
的极大值点
B.函数![]() 有且只有1个零点
有且只有1个零点
C.存在正实数![]() ,使得
,使得![]() 成立
成立
D.对任意两个正实数![]() ,
,![]() ,且
,且![]() ,若
,若![]() ,则
,则![]() .
.
【答案】BD
【解析】
A.求函数的导数,结合函数极值的定义进行判断
B.求函数的导数,结合函数的单调性,结合函数单调性和零点个数进行判断即可
C.利用参数分离法,构造函数g(x)![]() ,求函数的导数,研究函数的单调性和极值进行判断即可
,求函数的导数,研究函数的单调性和极值进行判断即可
D.令g(t)=f(2+t)﹣f(2﹣t),求函数的导数,研究函数的单调性进行证明即可
A.函数的 的定义域为(0,+∞),
函数的导数f′(x)![]() ,∴(0,2)上,f′(x)<0,函数单调递减,(2,+∞)上,f′(x)>0,函数单调递增,
,∴(0,2)上,f′(x)<0,函数单调递减,(2,+∞)上,f′(x)>0,函数单调递增,
∴x=2是f(x)的极小值点,即A错误;
B.y=f(x)﹣x![]() lnx﹣x,∴y′
lnx﹣x,∴y′![]() 1
1![]() 0,
0,
函数在(0,+∞)上单调递减,且f(1)﹣1![]() ln1﹣1=1>0,f(2)﹣2
ln1﹣1=1>0,f(2)﹣2![]() ln2﹣2= ln2﹣1<0,∴函数y=f(x)﹣x有且只有1个零点,即B正确;
ln2﹣2= ln2﹣1<0,∴函数y=f(x)﹣x有且只有1个零点,即B正确;
C.若f(x)>kx,可得k![]() ,令g(x)
,令g(x)![]() ,则g′(x)
,则g′(x)![]() ,
,
令h(x)=﹣4+x﹣xlnx,则h′(x)=﹣lnx,
∴在x∈(0,1)上,函数h(x)单调递增,x∈(1,+∞)上函数h(x)单调递减,
∴h(x)h(1)<0,∴g′(x)<0,
∴g(x)![]() 在(0,+∞)上函数单调递减,函数无最小值,
在(0,+∞)上函数单调递减,函数无最小值,
∴不存在正实数k,使得f(x)>kx恒成立,即C不正确;
D.令t∈(0,2),则2﹣t∈(0,2),2+t>2,
令g(t)=f(2+t)﹣f(2﹣t)![]() ln(2+t)
ln(2+t)![]() ln(2﹣t)
ln(2﹣t)![]() ln
ln![]() ,
,
则g′(t)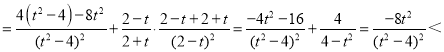 0,
0,
∴g(t)在(0,2)上单调递减,
则g(t)<g(0)=0,
令x1=2﹣t,
由f(x1)=f(x2),得x2>2+t,
则x1+x2>2﹣t+2+t=4,
当x2≥4时,x1+x2>4显然成立,
∴对任意两个正实数x1,x2,且x2>x1,若f(x1)=f(x2),则x1+x2>4,故D正确
故正确的是BD,
故选:BD.


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】为增强学生体质,合肥一中组织体育社团,某班级有4人积极报名参加篮球和足球社团,每人只能从两个社团中选择其中一个社团,大家约定:每个人通过掷一枚质地均匀的骰子决定自己参加哪个社团,掷出点数为5或6的人参加篮球社团,掷出点数小于5的人参加足球社团.
(1)求这4人中恰有1人参加篮球社团的概率;
(2)用![]() ,
,![]() 分别表示这4人中参加篮球社团和足球社团的人数,记随机变量X为
分别表示这4人中参加篮球社团和足球社团的人数,记随机变量X为![]() 和
和![]() 之差的绝对值,求随机变量X的分布列与数学期望
之差的绝对值,求随机变量X的分布列与数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)试用“五点法”画出函数![]() 在区间
在区间![]() 的简图;
的简图;
(2)指出该函数的图象可由![]() 的图象经过怎样的平移和伸缩变换得到?
的图象经过怎样的平移和伸缩变换得到?
(3)若![]() 时,函数
时,函数![]() 的最小值为
的最小值为![]() ,试求出函数
,试求出函数![]() 的最大值并指出
的最大值并指出![]() 取何值时,函数
取何值时,函数![]() 取得最大值.
取得最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知点
中,已知点![]() ,
,![]() ,
,![]() 为动点,且直线
为动点,且直线![]() 与直线
与直线![]() 的斜率之积为
的斜率之积为![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 相交于不同的两点
相交于不同的两点![]() ,
,![]() .若点
.若点![]() 在
在![]() 轴上,且
轴上,且![]() ,求点
,求点![]() 的纵坐标的取值范围.
的纵坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知函数![]() ,点
,点![]() 、
、![]() 分别是
分别是![]() 的图象与
的图象与![]() 轴、
轴、![]() 轴的交点,
轴的交点,![]() 、
、![]() 分别是
分别是![]() 的图象上横坐标为
的图象上横坐标为![]() 、
、![]() 的两点,
的两点,![]() 轴,且
轴,且![]() 、
、![]() 、
、![]() 三点共线.
三点共线.

(1)求函数![]() 的解析式;
的解析式;
(2)若![]() ,
,![]() ,求
,求![]() ;
;
(3)若关于![]() 的函数
的函数![]() 在区间
在区间![]() 上恰好有一个零点,求实数
上恰好有一个零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将![]() 颗珠子分成
颗珠子分成![]() 堆.若通过每次从其中
堆.若通过每次从其中![]() 堆中各取走一颗珠子,而最后取完,则称这样的分法为“和谐的”.试给出和谐分法的充分必要条件,并加以证明.
堆中各取走一颗珠子,而最后取完,则称这样的分法为“和谐的”.试给出和谐分法的充分必要条件,并加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以直角坐标系的原点为极点,以
为参数),以直角坐标系的原点为极点,以![]() 轴的正半轴为极轴建立极坐标系,已知直线
轴的正半轴为极轴建立极坐标系,已知直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程;
的普通方程;
(2)若![]() 与曲线
与曲线![]() 相切,且
相切,且![]() 与坐标轴交于
与坐标轴交于![]() 两点,求以
两点,求以![]() 为直径的圆的极坐标方程.
为直径的圆的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知焦点在![]() 轴上的抛物线
轴上的抛物线![]() 过点
过点![]() ,椭圆
,椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() ,其中
,其中![]() 与
与![]() 的焦点重合,过
的焦点重合,过![]() 与长轴垂直的直线交椭圆
与长轴垂直的直线交椭圆![]() 于
于![]() 两点且
两点且![]() ,曲线
,曲线![]() 是以原点为圆心以
是以原点为圆心以![]() 为半径的圆.
为半径的圆.
(1)求![]() 与
与![]() 及
及![]() 的方程;
的方程;
(2)若动直线![]() 与圆
与圆![]() 相切,且与
相切,且与![]() 交与
交与![]() 两点,三角形
两点,三角形![]() 的面积为
的面积为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com