
【题目】已知圆![]() 的方程为
的方程为![]() ,直线l的方程为
,直线l的方程为![]() ,点P在直线l上,过点P作圆
,点P在直线l上,过点P作圆![]() 的切线PA,PB,切点为A,B.
的切线PA,PB,切点为A,B.
(1)若![]() ,求点P的坐标;
,求点P的坐标;
(2)求证:经过A,P,![]() 三点的圆必经过异于
三点的圆必经过异于![]() 的某个定点,并求该定点的坐标.
的某个定点,并求该定点的坐标.
【答案】(1)![]() 和
和![]() ;(2)
;(2)![]() 和
和![]()
【解析】
(1)设![]() ,连接
,连接![]() ,分析易得
,分析易得![]() ,即有
,即有![]() ,解得
,解得![]() 的值,即可得到答案.
的值,即可得到答案.
(2)根据题意,分析可得:过A,P,![]() 三点的圆为以
三点的圆为以![]() 为直径的圆,设
为直径的圆,设![]() 的坐标为
的坐标为
![]() ,用
,用![]() 表示过A,P,
表示过A,P,![]() 三点的圆为
三点的圆为![]() ,结合直线与圆的位置关系,分析可得答案.
,结合直线与圆的位置关系,分析可得答案.
(1)根据题意,点P在直线l上,
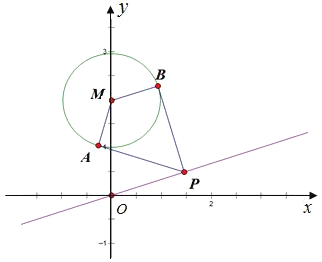
设![]() ,连接
,连接![]() ,
,
因为圆![]() 的方程为
的方程为![]() ,
,
所以圆心![]() ,半径
,半径![]() ,
,
因为过点P作圆![]() 的切线PA,PB,切点为A,B;
的切线PA,PB,切点为A,B;
则有 ,且
,且![]() ,
,
易得![]() ,
,
又由![]() ,即
,即![]() ,
,
则![]() ,即有
,即有![]() ,
,
解得![]() 或
或![]() ,即
,即![]() 的坐标为
的坐标为![]() 和
和![]() .
.
(2)根据题意,![]() 是圆
是圆![]() 的切线,则
的切线,则![]() ,
,
则过A,P,![]() 三点的圆为以
三点的圆为以![]() 为直径的圆,
为直径的圆,
设![]() 的坐标为
的坐标为![]() ,
,![]() ,
,
则以![]() 为直径的圆为
为直径的圆为![]() ,
,
变形可得:![]() ,
,
即![]() ,
,
则有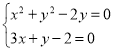 ,解得
,解得![]() 或
或![]() ,
,
则当![]() 和
和![]() ,
,![]() 时,
时,![]() 恒成立,
恒成立,
则经过A,P,![]() 三点的圆必经过异于
三点的圆必经过异于![]() 的某个定点,
的某个定点,
且定点的坐标![]() 和
和![]() .
.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).在以坐标原点
为参数).在以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,且与直角坐标系长度单位相同的极坐标系中,曲线
轴的正半轴为极轴,且与直角坐标系长度单位相同的极坐标系中,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() .若直
.若直![]() 与曲线
与曲线![]() 相交于两点
相交于两点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小型企业甲产品生产的投入成本x(单位:万元)与产品销售收入y(单位:万元)存在较好的线性关系,下表记录了最近5次该产品的相关数据.
x(万元) | 3 | 5 | 7 | 9 | 11 |
y(万元) | 8 | 10 | 13 | 17 | 22 |
(1)求y关于x的线性回归方程;
(2)根据(1)中的回归方程,判断该企业甲产品投入成本12万元的毛利率更大还是投入成本15万元的毛利率更大(毛利率![]()
![]()
![]() )?
)?
相关公式: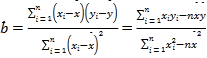 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题错误的是
A. 三棱锥的四个面可以都是直角三角形;
B. 等差数列{an}的前n项和为Sn(n=1,2,3…),若当首项a1和公差d变化时,a5+a8+a11是一个定值,则S16为定值;
C. ![]() 中,sinA>sinB是
中,sinA>sinB是![]() 的充要条件;
的充要条件;
D. 若双曲线的渐近线互相垂直,则这条双曲线是等轴双曲线.
查看答案和解析>>
科目:高中数学 来源: 题型:
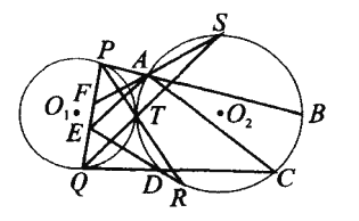
【题目】如图,两圆外切于点T, PQ为![]() 的弦,直线PT、QT分别交
的弦,直线PT、QT分别交![]() 于点R、S,分别过P、Q作
于点R、S,分别过P、Q作![]() 的切线依次交
的切线依次交![]() 于A、B、D、C,直线RD、SA分别交PQ于E、F。求证:
于A、B、D、C,直线RD、SA分别交PQ于E、F。求证:![]() 。
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com