
【题目】在三棱锥![]() 中,
中,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,点
,点![]() 在棱
在棱![]() 上.
上.
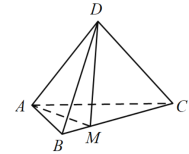
![]() 若
若![]() 为
为![]() 的中点,证明:
的中点,证明:![]() .
.
![]() 若
若![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求
,求![]() .
.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1的参数方程为![]() (
(![]() 为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为
为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为![]() .
.
(1)写出曲线C1和C2的直角坐标方程;
(2)已知P为曲线C2上的动点,过点P作曲线C1的切线,切点为A,求|PA|的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在国家批复成立江北新区后,南京市政府规划在新区内的一条形地块上新建一个全民健身中心,规划区域为四边形ABCD,如图![]() ,
,![]() ,点B在线段OA上,点C、D分别在射线OP与AQ上,且A和C关于BD对称.已知
,点B在线段OA上,点C、D分别在射线OP与AQ上,且A和C关于BD对称.已知![]() .
.
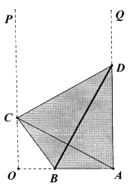
(1)若![]() ,求BD的长;
,求BD的长;
(2)问点C在何处时,规划区域的面积最小?最小值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过抛物线![]() 上一点
上一点![]() 作直线交抛物线E于另一点N.
作直线交抛物线E于另一点N.
(1)若直线MN的斜率为1,求线段![]() 的长.
的长.
(2)不过点M的动直线l交抛物线E于A,B两点,且以AB为直径的圆经过点M,问动直线l是否恒过定点.如果有求定点坐标,如果没有请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】厂家在产品出厂前,需对产品做检验,第一次检测厂家的每件产品合格的概率为![]() ,如果合格,则可以出厂;如果不合格,则进行技术处理,处理后进行第二次检测.每件产品的合格率为
,如果合格,则可以出厂;如果不合格,则进行技术处理,处理后进行第二次检测.每件产品的合格率为![]() ,如果合格,则可以出厂,不合格则当废品回收.
,如果合格,则可以出厂,不合格则当废品回收.
![]() 求某件产品能出厂的概率;
求某件产品能出厂的概率;
![]() 若该产品的生产成本为
若该产品的生产成本为![]() 元/件,出厂价格为
元/件,出厂价格为![]() 元/件,每次检测费为
元/件,每次检测费为![]() 元/件,技术处理每次
元/件,技术处理每次![]() 元/件,回收获利
元/件,回收获利![]() 元/件.假如每件产品是否合格相互独立,记
元/件.假如每件产品是否合格相互独立,记![]() 为任意一件产品所获得的利润,求随机变量
为任意一件产品所获得的利润,求随机变量![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线C的参数方程为
中,曲线C的参数方程为![]() (
(![]() 为参数),以原点O为极点,x轴正半轴为极轴建立极坐标系,直线
为参数),以原点O为极点,x轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,且直线
,且直线![]() 与曲线C有两个不同的交点.
与曲线C有两个不同的交点.
(1)求实数a的取值范围;
(2)已知M为曲线C上一点,且曲线C在点M处的切线与直线![]() 垂直,求点M的直角坐标.
垂直,求点M的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某便利店统计了今年第一季度各个品类的销售收入占比和净利润占比,并将部分品类的这两个数据制成如下统计图(注:销售收入占比![]() ,净利润占比
,净利润占比![]() ,净利润
,净利润![]() 销售收入
销售收入![]() 成本
成本![]() 各类费用),现给出下列判断:
各类费用),现给出下列判断:
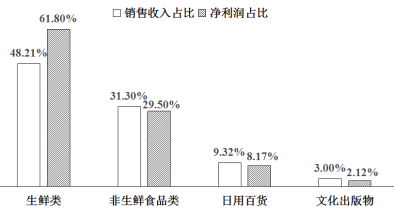
①该便利店第一季度至少有一种品类是亏损的;
②该便利店第一季度的销售收入中“生鲜类”贡献最大;
③该便利店第一季度“非生鲜食品类”的净利润一定高于“日用百货”的销售收入;
④该便利店第一季度“生鲜类”的销售收入比“非生鲜食品类”的销售收入多![]() .
.
则上述判断中正确的是( )
A.①②B.②③C.①④D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知点![]() 是
是![]() 轴下方(不含
轴下方(不含![]() 轴)一点,抛物线
轴)一点,抛物线![]() 上存在不同的两点
上存在不同的两点![]() 、
、![]() 满足
满足![]() ,
,![]() ,其中
,其中![]() 为常数,且
为常数,且![]() 、
、![]() 两点均在
两点均在![]() 上,弦
上,弦![]() 的中点为
的中点为![]() .
.
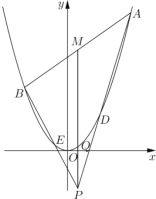
(1)若![]() 点坐标为
点坐标为![]() ,
,![]() 时,求弦
时,求弦![]() 所在的直线方程;
所在的直线方程;
(2)在(1)的条件下,如果过![]() 点的直线
点的直线![]() 与抛物线
与抛物线![]() 只有一个交点,过
只有一个交点,过![]() 点的直线
点的直线![]() 与抛物线
与抛物线![]() 也只有一个交点,求证:若
也只有一个交点,求证:若![]() 和
和![]() 的斜率都存在,则
的斜率都存在,则![]() 与
与![]() 的交点
的交点![]() 在直线
在直线![]() 上;
上;
(3)若直线![]() 交抛物线
交抛物线![]() 于点
于点![]() ,求证:线段
,求证:线段![]() 与
与![]() 的比为定值,并求出该定值.
的比为定值,并求出该定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com