
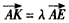 ,KF与平面ABG所成角为30°,求λ的值。
,KF与平面ABG所成角为30°,求λ的值。 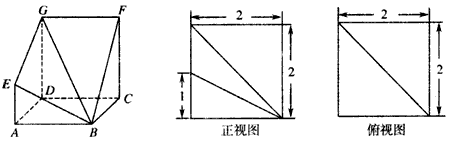
解:(Ⅰ)连接AC,BD,在正方形ABCD中,AC⊥BD,
又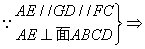 GD⊥面ABCD,
GD⊥面ABCD,
又AC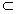 面ABCD,
面ABCD,
则AC⊥GD,
又AC⊥BD,GD∩BD=D,
则AC⊥面BDG,
又AC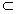 面AEFC,
面AEFC,
故面AEFC⊥面BDG;
(Ⅱ)由三视图知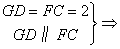 四边形DCFG为平行四边形
四边形DCFG为平行四边形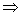 FG∥CD且FG=CD,
FG∥CD且FG=CD,
在正方形ABCD中,AB∥CD且AB=CD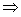
FG∥AB且FG=AB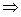 A,B,G,F共面
A,B,G,F共面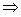 平面ABG,
平面ABG,
即平面ABFG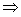 KF∩平面ABG=F,
KF∩平面ABG=F,
作KO⊥AG于O,连接FO, AB⊥平面AEGD,
AB⊥平面AEGD,
又AE∥GD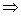 AE,GD共面于AEGD,
AE,GD共面于AEGD,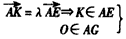
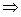 KO
KO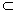 平面AEGD
平面AEGD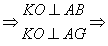 KO⊥平面ABG
KO⊥平面ABG FO为KF在平面ABC的射影
FO为KF在平面ABC的射影 ∠KFO为KF与平面ABG所成角,
∠KFO为KF与平面ABG所成角,
由已知可得∠KFO=30°,AE=1,
∴AK=λ,
由三视图知AD=DG=2,
∴∠DAG=45°,
∴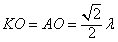 ,∴
,∴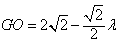 ,
,
∴Rt△FGO中,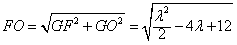 ,
,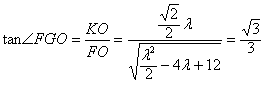 ,
,
∴λ=2或λ=-6(舍)。


科目:高中数学 来源: 题型:

| AK |
| AE |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年东北师大附中、哈师大附中、辽宁实验中学高三第二次模拟考试数学理卷 题型:解答题
((本小题满分12分)
如图,多面体ABCD—EFG中,底面ABCD为正方形,GD//FC//AE,AE⊥平面ABCD,其正视图、俯视图如下:

(I)求证:平面AEF⊥平面BDG;
(II)若存在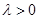 使得
使得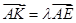 ,二面角A—BG—K的大小为
,二面角A—BG—K的大小为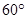 ,求
,求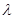 的值。
的值。
查看答案和解析>>
科目:高中数学 来源:2010-2011年浙江省高二下学期期中考试理数试题 题型:选择题
((本小题满分12分)
如图,多面体ABCD—EFG中,底面ABCD为正方形,GD//FC//AE,AE⊥平面ABCD,其正视图、俯视图如下:
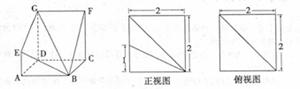
(I)求证:平面AEF⊥平面BDG;
(II)若存在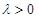 使得
使得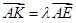 ,二面角A—BG—K的大小为
,二面角A—BG—K的大小为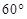 ,求
,求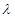 的值。
的值。
查看答案和解析>>
科目:高中数学 来源:2010-2011年东北师大附中、哈师大附中、辽宁实验中学高二第二次考试数学理卷 题型:解答题
(本小题满分12分)
如图,多面体ABCD—EFG中,底面ABCD为正方形,GD//FC//AE,AE⊥平面ABCD,其正视图、俯视图如下:
(I)求证:平面AEF⊥平面BDG;

(II)若存在 使得
使得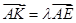 ,二面角A—BG—K的大小为
,二面角A—BG—K的大小为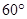 ,求
,求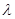 的值。
的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com