
【题目】定义区间![]() ,
,![]() ,
,![]() ,
,![]() 的长度均为
的长度均为![]() ,多个区间并集的长度为各区间长度之和,例如,
,多个区间并集的长度为各区间长度之和,例如, ![]() 的长度
的长度![]() . 用
. 用![]() 表示不超过
表示不超过![]() 的最大整数,记
的最大整数,记![]() ,其中
,其中![]() .设
.设![]() ,
,![]() ,当
,当![]() 时,不等式
时,不等式![]() 解集区间的长度为
解集区间的长度为![]() ,则
,则![]() 的值为
的值为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
先化简f(x)=[x]{x}=[x](x﹣[x])=[x]x﹣[x]2,再化简f(x)<g(x),再分类讨论:①当x∈[0,1)时,②当x∈[1,2)时③当x∈[2,3)时,从而得出f(x)<g(x)在0≤x≤k时的解集的长度,依题意即可求得k的值.
f(x)=[x]{x}=[x](x﹣[x])=[x]x﹣[x]2,g(x)=x﹣1,
f(x)<g(x)[x]x﹣[x]2<x﹣1即([x]﹣1)x<[x]2﹣1,
当x∈[0,1)时,[x]=0,上式可化为x>1,
∴x∈;
当x∈[1,2)时,[x]=1,上式可化为0>0,
∴x∈;
当x∈[2,3)时,[x]=2,[x]﹣1>0,上式可化为x<[x]+1=3,
∴当x∈[0,3)时,不等式f(x)<g(x)解集区间的长度为d=3﹣2=1;
同理可得,当x∈[3,4)时,不等式f(x)<g(x)解集区间的长度为d=4﹣2=2;
∵不等式f(x)<g(x)解集区间的长度为5,
∴k﹣2=5,∴k=7.
故答案为:B.


科目:高中数学 来源: 题型:
【题目】近年来,“共享单车”的出现为市民“绿色出行”提供了极大的方便,某共享单车公司计划在甲、乙两座城市共投资240万元,根据行业规定,每个城市至少要投资80万元,由前期市场调研可知:甲城市收益![]() 与投入
与投入![]() (单位:万元)满足
(单位:万元)满足![]() ,乙城市收益
,乙城市收益![]() 与投入
与投入![]() (单位:万元)满足
(单位:万元)满足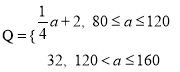 ,设甲城市的投入为
,设甲城市的投入为![]() (单位:万元),两个城市的总收益为
(单位:万元),两个城市的总收益为![]() (单位:万元).
(单位:万元).
(1)当投资甲城市128万元时,求此时公司总收益;
⑵试问如何安排甲、乙两个城市的投资,才能使公司总收益最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某群体的人均通勤时间,是指单日内该群体中成员从居住地到工作地的平均用时.某地上班族![]() 中的成员仅以自驾或公交方式通勤.分析显示:当
中的成员仅以自驾或公交方式通勤.分析显示:当![]() 中
中![]() (
(![]() )的成员自驾时,自驾群体的人均通勤时间为
)的成员自驾时,自驾群体的人均通勤时间为 (单位:分钟),而公交群体的人均通勤时间不受
(单位:分钟),而公交群体的人均通勤时间不受![]() 影响,恒为
影响,恒为![]() 分钟,试根据上述分析结果回答下列问题:
分钟,试根据上述分析结果回答下列问题:
(1)当![]() 在什么范围内时,公交群体的人均通勤时间少于自驾群体的人均通勤时间?
在什么范围内时,公交群体的人均通勤时间少于自驾群体的人均通勤时间?
(2)求该地上班族![]() 的人均通勤时间
的人均通勤时间![]() 的表达式;讨论
的表达式;讨论![]() 的单调性,并说明其实际意义.
的单调性,并说明其实际意义.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知圆![]() 的方程为
的方程为![]() ,圆
,圆![]() 的方程为
的方程为![]() ,动圆
,动圆![]() 与圆
与圆![]() 内切且与圆
内切且与圆![]() 外切.
外切.
(1)求动圆圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)已知![]() 与
与![]() 为平面内的两个定点,过
为平面内的两个定点,过![]() 点的直线
点的直线![]() 与轨迹
与轨迹![]() 交于
交于![]() ,
,![]() 两点,求四边形
两点,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() :
: (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 的直角坐标为
的直角坐标为![]() ,直线
,直线![]() 与曲线
与曲线![]() 的交点为
的交点为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com