
【题目】设直线l过点P(0,3),和椭圆 ![]() 交于A、B两点(A在B上方),试求
交于A、B两点(A在B上方),试求 ![]() 的取值范围 .
的取值范围 .
【答案】[ ![]() )
)
【解析】解:当直线l的斜率不存在时,A点坐标为(0,2),B点坐标为(0,﹣2),这时 ![]() =
= ![]() .
.
当直线l斜率为k时,直线l方程为y=kx+3,
设A点坐标为(x1,y1),B点坐标为(x2,y2),则向量AP=(﹣x1,3﹣y1),向量PB=(x2,y2﹣3),
所以 ![]() =
= ![]() ,
,
因为直线y=kx+3与椭圆有两个交点,且它们的横坐标不同,
把y=kx+3代入 ![]() 后的一元二次方程(9k2+4)x2+54k+45=0的判别式(54k)2﹣4(9k2+4)×45>0,
后的一元二次方程(9k2+4)x2+54k+45=0的判别式(54k)2﹣4(9k2+4)×45>0,
所以k> ![]() 或k<﹣
或k<﹣ ![]() ,
,
设 ![]() =λ,则x1=λx2,
=λ,则x1=λx2,
因为x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]() ,
,
所以(1+λ)x2═﹣ ![]() ,(1)
,(1)
λx22= ![]() ,(2)
,(2)
显然λ不等于1,解得0<λ<1.
综上所述 ![]() 的范围是[
的范围是[ ![]() ).
).
所以答案是:[ ![]() ).
).


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知正项等比数列{an}满足:a7=a6+2a5 , 若存在两项am , an , 使得 ![]() =4a1 , 则
=4a1 , 则 ![]() +
+ ![]() 的最小值为( )
的最小值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)= ![]() e3x+me2x+(2m+1)ex+1有两个极值点,则实数m的取值范围是( )
e3x+me2x+(2m+1)ex+1有两个极值点,则实数m的取值范围是( )
A.(﹣ ![]() ,1﹣
,1﹣ ![]() )
)
B.[﹣ ![]() ,1﹣
,1﹣ ![]() ]
]
C.(﹣∞,1﹣ ![]() )
)
D.(﹣∞,1﹣ ![]() )∪(1+
)∪(1+ ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知球内接四棱锥P﹣ABCD的高为3,AC,BC相交于O,球的表面积为 ![]() ,若E为PC中点.
,若E为PC中点. 
(1)求证:OE∥平面PAD;
(2)求二面角A﹣BE﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知复数z1=m+ni(m,n∈R),z=x+yi(x,y∈R),z2=2+4i且 ![]() .
.
(1)若复数z1对应的点M(m,n)在曲线 ![]() 上运动,求复数z所对应的点P(x,y)的轨迹方程;
上运动,求复数z所对应的点P(x,y)的轨迹方程;
(2)将(1)中的轨迹上每一点按向量 ![]() 方向平移
方向平移 ![]() 个单位,得到新的轨迹C,求C的轨迹方程;
个单位,得到新的轨迹C,求C的轨迹方程;
(3)过轨迹C上任意一点A(异于顶点)作其切线,交y轴于点B,求证:以线段AB为直径的圆恒过一定点,并求出此定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,设点M(x0 , y0)是椭圆C: ![]() +y2=1上一点,从原点O向圆M:(x﹣x0)2+(y﹣y0)2=r2作两条切线分别与椭圆C交于点P,Q.直线OP,OQ的斜率分别记为k1 , k2
+y2=1上一点,从原点O向圆M:(x﹣x0)2+(y﹣y0)2=r2作两条切线分别与椭圆C交于点P,Q.直线OP,OQ的斜率分别记为k1 , k2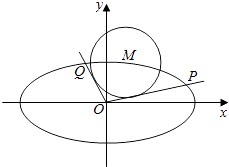
(1)若圆M与x轴相切于椭圆C的右焦点,求圆M的方程;
(2)若r= ![]() ,①求证:k1k2=﹣
,①求证:k1k2=﹣ ![]() ;②求OPOQ的最大值.
;②求OPOQ的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某职业学校的王亮同学到一家贸易公司实习,恰逢该公司要通过海运出口一批货物,王亮同学随公司负责人到保险公司洽谈货物运输期间的投保事宜,保险公司提供了缴纳保险费的两种方案:
①一次性缴纳50万元,可享受9折优惠;
②按照航行天数交纳:第一天缴纳0.5元,从第二天起每天交纳的金额都是其前一天的2倍,共需交纳20天.
请通过计算,帮助王亮同学判断那种方案交纳的保费较低.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com