练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】若函数f（x）定义在R上的奇函数，且在（﹣∞，0）上是增函数，又f（2）=0，则不等式xf（x+1）＜0的解集为 ．

    【答案】（0，1）∪（﹣3，﹣1）
    【解析】解：∵函数f（x）定义在R上的奇函数，且在（﹣∞，0）上是增函数，又f（2）=0， ∴f（x）在（0，+∞）上是增函数，且f（﹣2）=﹣f（2）=0，
    ∴当x＞2或﹣2＜x＜0时，f（x）＞0，当x＜﹣2或0＜x＜2时，f（x）＜0，（如图）
    则不等式xf（x+1）＜0等价为
    或 ，
    即 或 ，
    则 或 ，
    解得0＜x＜1或﹣3＜x＜﹣1，
    故不等式的解集为（0，1）∪（﹣3，﹣1），
    所以答案是：（0，1）∪（﹣3，﹣1）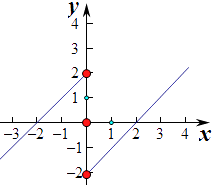

    【考点精析】掌握奇偶性与单调性的综合是解答本题的根本，需要知道奇函数在关于原点对称的区间上有相同的单调性；偶函数在关于原点对称的区间上有相反的单调性．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知椭圆和直线： ，椭圆的离心率，坐标原点到直线的距离为.

    （Ⅰ）求椭圆的方程；

    （Ⅱ）已知定点，若直线过点且与椭圆相交于两点，试判断是否存在直线，使以为直径的圆过点？若存在，求出直线的方程；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在直四棱柱ABCD﹣A1B1C1D1中，底面是边长为 的正方形，AA1=3，点F在棱B1B上运动．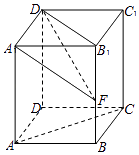

    （1）若三棱锥B1﹣A1D1F的体积为 时，求异面直线AD与D1F所成的角
    （2）求异面直线AC与D1F所成的角．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】将一张纸沿直线l对折一次后，点A（0，4）与点B（8，0）重叠，点C（6，8）与点D（m，n）重叠．
    （1）求直线l的方程；
    （2）求m+n的值；
    （3）直线l上是否存在一点P，使得||PB|﹣|PC||存在最大值，如果存在，请求出最大值，以及此时点P的坐标；如果不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数， .

    （1） 关于的方程在区间上有解,求的取值范围；

    （2） 当时， 恒成立,求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数f（x）的定义域为D，若存在非零实数m，使得对于任意x∈M（MD），有（x﹣m）∈D且f（x﹣m）≤f（x），则称f（x）为M上的m度低调函数．如果定义域为R的函数f（x）是奇函数，当x≥0时，f（x）=|x﹣a2|﹣a2 ， 且f（x）为R上的5度低调函数，那么实数a的取值范围为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】用数学归纳法证明12+22+…+（n﹣1）2+n2+（n﹣1）2+…+22+12═ 时，由n=k的假设到证明n=k+1时，等式左边应添加的式子是（ ）
    A.（k+1）2+2k2
    B.（k+1）2+k2
    C.（k+1）2
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    在直角坐标系中，曲线的参数方程为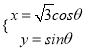（为参数），以坐标原点为极点，以轴正半轴为极轴，建立极坐标系，曲线的极坐标方程为.

    （1）写出的普通方程和的直角坐标方程；

    （2）设点在上，点在上，求的最小值及此时的直角坐标.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知为常数， ，函数， （其中是自然对数的底数）.

    （1）过坐标原点作曲线的切线，设切点为，求证： ；

    （2）令，若函数在区间上是单调函数，求的取值范围．

    查看答案和解析>>

    同步练习册答案