
【题目】在平面直角坐标系内,已知A(1,a),B(﹣5,﹣3),C(4,0);
(1)当a∈( ![]() ,3)时,求直线AC的倾斜角α的取值范围;
,3)时,求直线AC的倾斜角α的取值范围;
(2)当a=2时,求△ABC的BC边上的高AH所在直线方程l.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,满足x2+y2≤1,x≥0,y≥0的点P(x,y)的集合对应的平面图形的面积为 ![]() ;类似的,在空间直角坐标系O﹣xyz中,满足x2+y2+z2≤1,x≥0,y≥0,z≥0的点P(x,y,z)的集合对应的空间几何体的体积为( )
;类似的,在空间直角坐标系O﹣xyz中,满足x2+y2+z2≤1,x≥0,y≥0,z≥0的点P(x,y,z)的集合对应的空间几何体的体积为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB切⊙O于点B,直线AO交⊙O于D,E两点,BC⊥DE,垂足为C.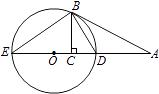
(1)证明:∠CBD=∠DBA;
(2)若AD=3DC,BC= ![]() ,求⊙O的直径.
,求⊙O的直径.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的多面体,它的正视图为直角三角形,侧视图为正三角形,俯视图为正方形(尺寸如图所示),E为VB的中点. 
(1)求证:VD∥平面EAC;
(2)求二面角A﹣VB﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给n个自上而下相连的正方形着黑色或白色.当n≤4时,在所有不同的着色方案中,黑色正方形互不相邻的着色方案如图所示,由此推断,当n=6时,至少有两个黑色正方形相邻的着色方案共有( )种. 
A.21
B.32
C.43
D.54
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知y=f(x)是定义在R上的奇函数,当x≥0时,f(x)=x+x2 .
(1)求x<0时,f(x)的解析式;
(2)问是否存在这样的非负数a,b,当x∈[a,b]时,f(x)的值域为[4a﹣2,6b﹣6]?若存在,求出所有的a,b值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com