
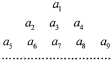 已知an=($\frac{1}{3}$)n,把数列{an}的各项排列成如下的三角形状:记A(m,n)表示第m行的第n个数,则A(11,2)( )
已知an=($\frac{1}{3}$)n,把数列{an}的各项排列成如下的三角形状:记A(m,n)表示第m行的第n个数,则A(11,2)( )| A. | ($\frac{1}{3}$)67 | B. | ($\frac{1}{3}$)68 | C. | ($\frac{1}{3}$)101 | D. | ($\frac{1}{3}$)102 |
分析 ①A(11,2)为三角形状的第11行的第2个数,根据题意得第11行的最后一个数是a121;
②且有2×11-1=21个项,得到第11行得第一项为101+2-1=102,所以为a102求出即可
解答 解:由A(m,n)表示第m行的第n个数可知,A(11,2)表示第11行的第2个数,
根据图形可知:①每一行的最后一个项的项数为行数的平方,所以第11行的最后一个项的项数为112=121,即为a121;
②每一行都有2n-1个项,所以第11行有2×11-1=21个项,得到第11行第一个项为121-21+1=101,所以第12项的项数为101+2-1=102;
所以A(11,2)=a102=($\frac{1}{3}$)102,
故选:D.
点评 考查学生利用数列的递推式解决数学问题的能力,会根据图形归纳总计得到一组数的规律.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
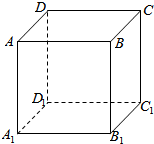 如图所示,在正方形ABCD-A1B1C1D1中:
如图所示,在正方形ABCD-A1B1C1D1中:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,±$\sqrt{12-2k}$) | B. | (±$\sqrt{12-2k}$,0) | C. | (0,±2) | D. | (±2,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “所有金属都能导电,铁是金属,所以铁能导电”这种推理属于演绎推理 | |
| B. | 已知数据x1,x2,…,xn的方差是4,则数据-3x1+2015,-3x2+2015,…,-3xn+2015的标准差是6 | |
| C. | 用相关指数R2来刻画回归效果,R2的值越小,说明模型的拟合效果越好 | |
| D. | 若变量y和x之间的相关系数r=-0.9362,则变量y和x之间具有很强的线性相关关系 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-4,1] | B. | [0,5] | C. | [-4,1]∪[0,5] | D. | [-2,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com